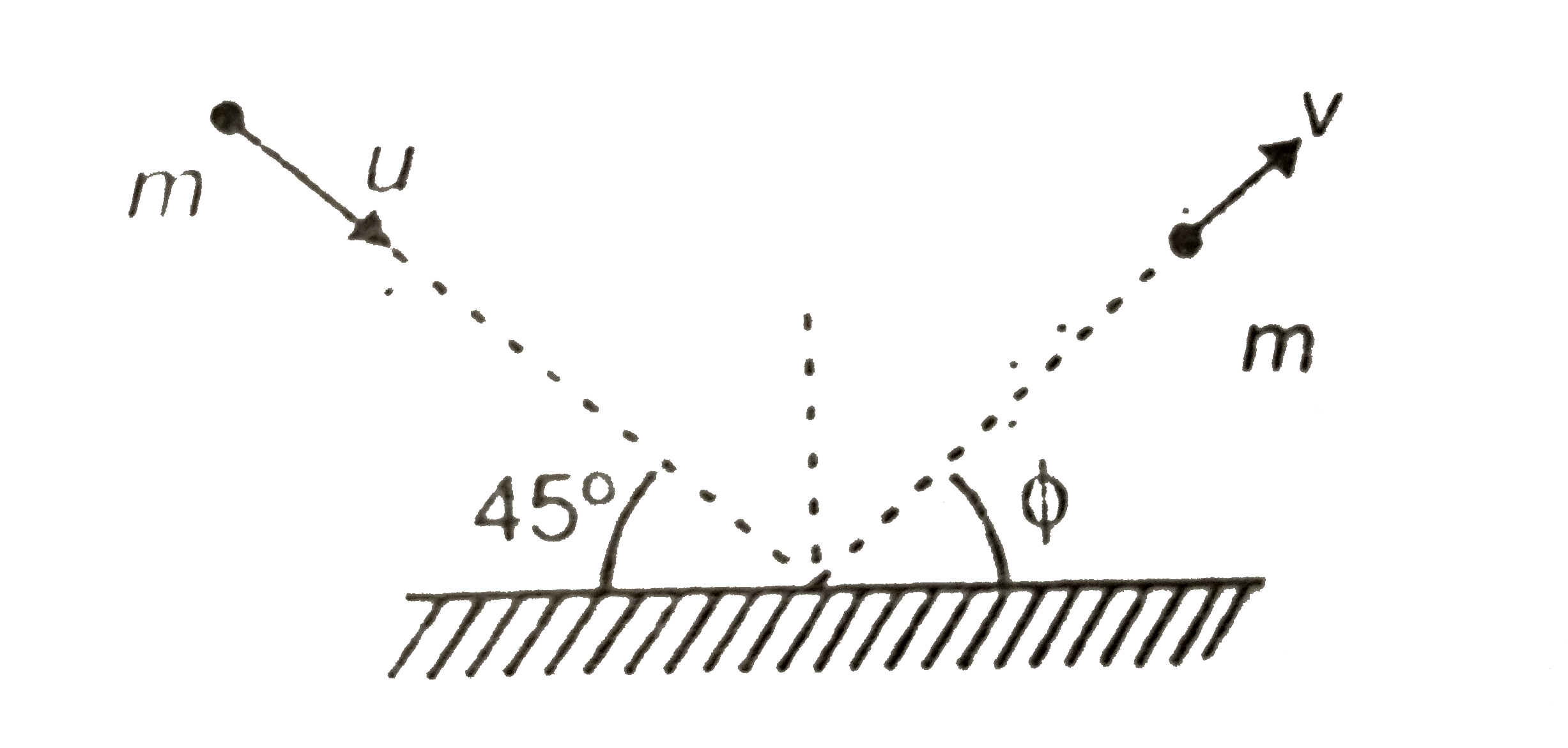
A particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45∘. The particle rebounds at an angle ϕ with speed v. If coefficient of restituion is 1√3, then angle ϕ is
The correct Answer is:2
−A+−B=a[(1+cosωt)ˆi+sinωtˆj],−A−−B=a[(1−cosωt)ˆi−sinωtˆj]
∣∣∣−A+−B∣∣∣=a∣∣∣2cos(ωt2)∣∣∣,∣∣∣−A−−B∣∣∣=a∣∣∣2sin(ωt2)∣∣∣
∣∣
∣∣−A+−BA−B∣∣
∣∣=∣∣∣cot(ωt2)∣∣∣=√3⇒ωt2=π6⇒t=2
Topper's Solved these Questions
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - JEE Main (Archive)
19 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
Similar Questions
A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
View SolutionA cricket ball is hit for a six the bat at an angle of 45∘ to the horizontal with kinetic energy K. At the highest point, the kinetic energy of the ball is
View SolutionA particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
View SolutionThe angle of dip is the angle
View SolutionA ball is thrown onto a smooth floor with speed u at angle θ=45∘. If it rebounds with a speed v at the same angle ϕ=45∘. Then the coefficient of restitution is

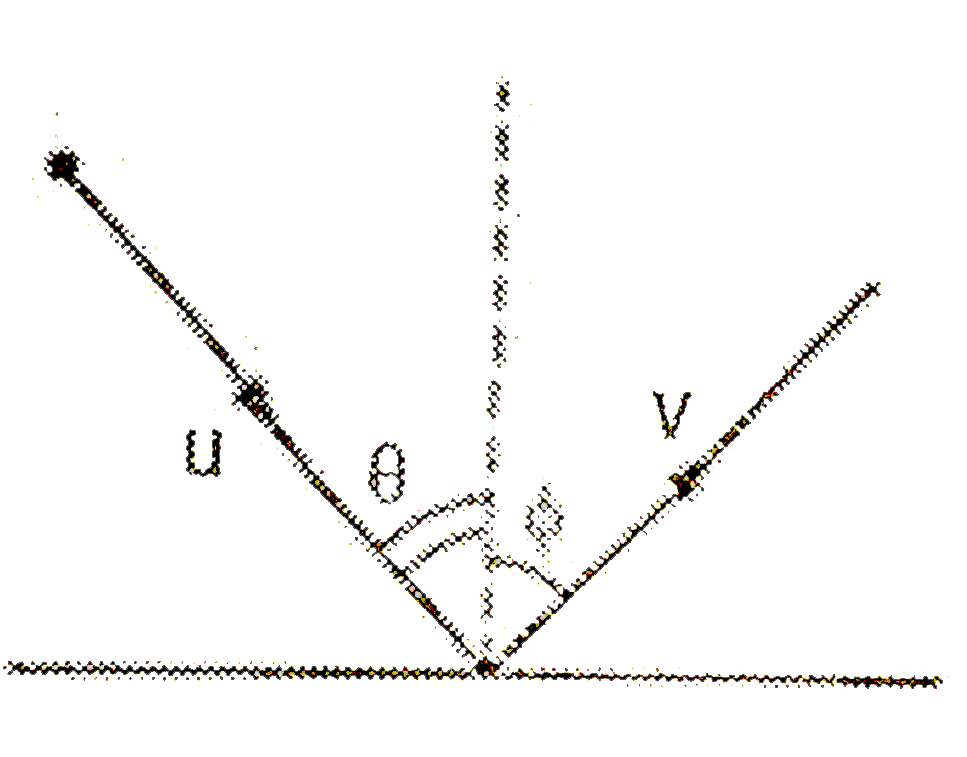
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle theta with the vertical, and rebounds with a speed upsilon , at an angle phi with the vertical. The coefficient of restitution between the particle and the floor is e. The angle phi is equal to :
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ to the vertical, and rebounds with a speed v, at an angle ϕ to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is
View SolutionA particle is thrown with a speed u at an angle θ with the horizontal. When the particle makes an angle ϕ with the horizontal. Its speed changes to v :
View SolutionA particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45^(@) . The particle rebounds at an angle phi with speed v . If coefficient of restituion is (1)/(sqrt(3)) , then angle phi is
View SolutionA particle strikes a smooth horizontal surface at an angle θ>0 and it rebounds at an angle ϕ as shown

View SolutionA particles strikes a smooth surface at an angle theta and rebounds at an angle phi . Coefficient of restitution is 0 lt e lt 1 , then STATEMENT-1 : If the same particle is thrown at angle phi , it will rebound at an angle theta . and STATEMENT-2 : phi is greater than theta .
View SolutionA particle strikes a horizontal smooth floor with a velocity u making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. The coefficient of restitution between the particle and the floor is e.
View SolutionA particle of mass m strikes a horizontal smooth floor with a velocity u making an angle 'θ' with the floor and rebound with velocity v making an angle 'ϕ' with the floor. The coefficient of restitution between the particle and the floor is e. Then
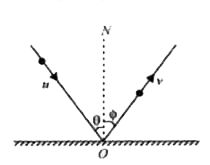
View SolutionA particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is
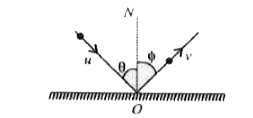
View SolutionA particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The angle ϕ is equal to
View SolutionA particle is thrown with a speed is at an angle θ with the horizontal. When the particle makes an angle ϕ with the horizontal, its speed changes to v, then
View Solution

