A circular road of radius 50 m has the angel of banking equal to 300. At what speed should a vehicle go on this road so that the friction is not used?
25 m/s
17 m/s
6 m/s
11 m/s
The correct Answer is:B
To solve the problem of determining the speed at which a vehicle should travel on a banked circular road without relying on friction, we can follow these steps:
Step 1: Understand the Forces Acting on the Vehicle
When a vehicle is on a banked circular road, the forces acting on it include:
- The gravitational force (mg) acting downwards.
- The normal force (N) acting perpendicular to the surface of the road.
- The centripetal force required for circular motion, which is provided by the horizontal component of the normal force.
Step 2: Set Up the Banking Angle and Radius
Given:
- Radius of the circular road, r=50m
- Angle of banking, θ=30∘
Step 3: Write the Equations for Forces
For the vehicle to move in a circle without friction, the following equations must hold:
1. The vertical forces must balance:
Ncosθ=mg
2. The horizontal forces provide the centripetal force:
Nsinθ=mv2r
Step 4: Eliminate Normal Force (N)
From the first equation, we can express N:
N=mgcosθ
Substituting N into the second equation:
mgcosθsinθ=mv2r
Step 5: Simplify the Equation
Cancel m from both sides:
gsinθcosθ=v2r
This can be rewritten using the tangent function:
gtanθ=v2r
Step 6: Solve for Speed (v)
Rearranging the equation gives:
v2=grtanθ
Substituting g=10m/s2, r=50m, and θ=30∘:
tan30∘=1√3
Thus,
v2=10⋅50⋅1√3=500√3
Step 7: Calculate the Speed
Taking the square root:
v=√500√3
Calculating this gives:
v≈16.99m/s≈17m/s
Final Answer
The speed at which the vehicle should go on this road so that friction is not used is approximately 17 m/s.
---
When a vehicle is on a banked circular road, the forces acting on it include:
- The gravitational force (mg) acting downwards.
- The normal force (N) acting perpendicular to the surface of the road.
- The centripetal force required for circular motion, which is provided by the horizontal component of the normal force.
Given:
- Radius of the circular road, r=50m
- Angle of banking, θ=30∘
For the vehicle to move in a circle without friction, the following equations must hold:
1. The vertical forces must balance:
Ncosθ=mg
2. The horizontal forces provide the centripetal force:
Nsinθ=mv2r
From the first equation, we can express N:
N=mgcosθ
Substituting N into the second equation:
mgcosθsinθ=mv2r
Cancel m from both sides:
gsinθcosθ=v2r
This can be rewritten using the tangent function:
gtanθ=v2r
Rearranging the equation gives:
v2=grtanθ
Substituting g=10m/s2, r=50m, and θ=30∘:
tan30∘=1√3
Thus,
v2=10⋅50⋅1√3=500√3
Taking the square root:
v=√500√3
Calculating this gives:
v≈16.99m/s≈17m/s
The speed at which the vehicle should go on this road so that friction is not used is approximately 17 m/s.
Topper's Solved these Questions
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2
49 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )
16 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 0 (LONG ANSWER TYPE)
4 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G
10 Videos
Similar Questions
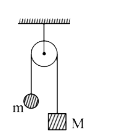
In the figure shown, a particle of small mass m is joined to a very heavy mass M (M >> m) by a light string passing over a light pulley. The total downward force on the pulley by the string is :
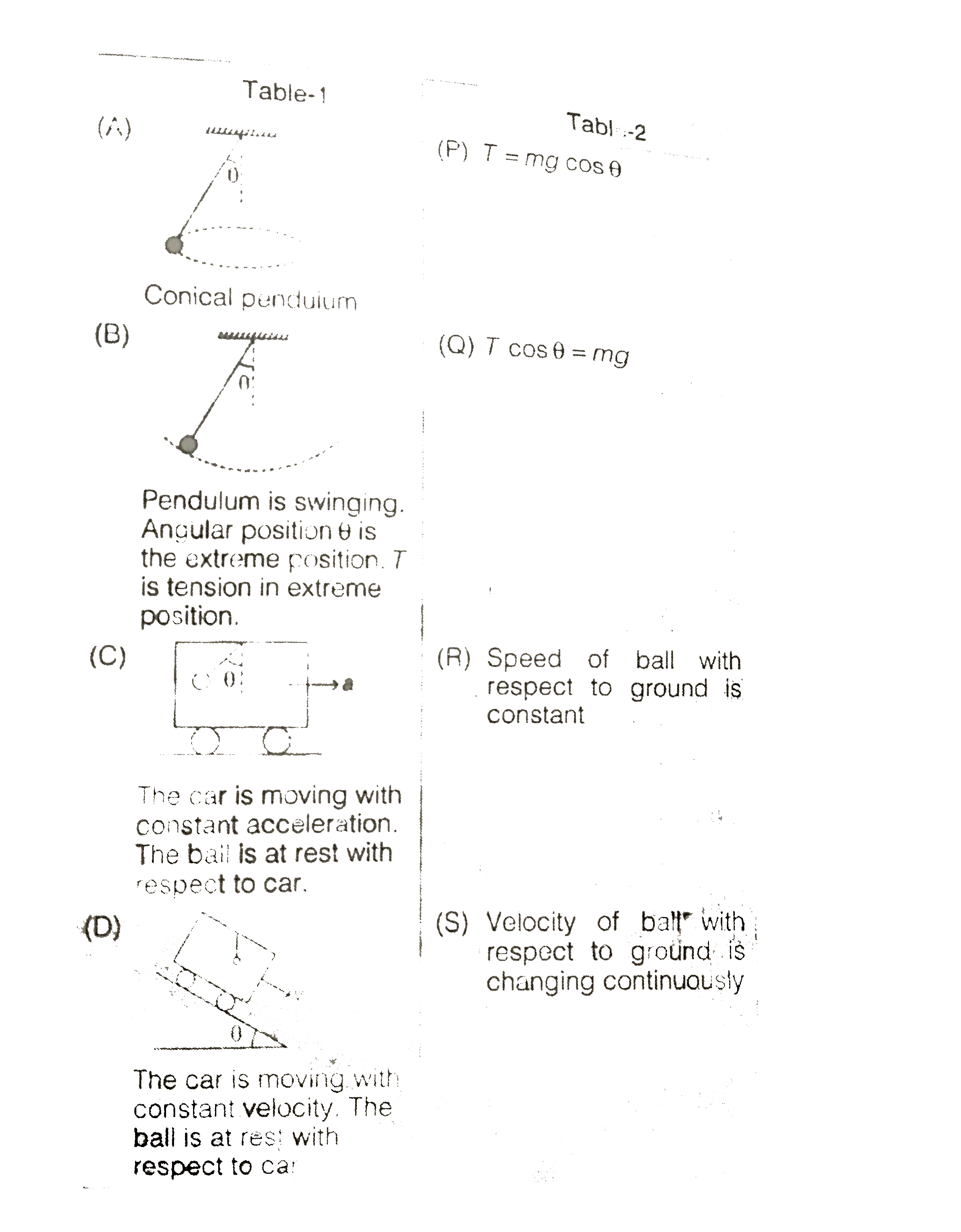
View SolutionIn all the four situations depicted in Table-1, a ball of mass m is connected to a string. In each case, find the tension in the string and match the appropriate entries is Table-2
View SolutionA block A of mass 14 kg moves alongg an inclined plance that makes an angle of 30∘ with the horizontal . This block is connected to another block B of mass 14 kg by a taut massless string that runs around a massless frictionless pulley . The block B moves down with constant velocity . Calculate force of friction and coefficient of kinetic friction .
View SolutionThe temperature coefficient of resistance of a wire is 0.00125 per ∘C. At 300 K, its resistance is 1Ω. The resistance of the wire will be 2Ω at
View SolutionWhat will increase in step-down transformer?
View SolutionThe road at a circular turn of radius 10 m is banked by an angle of 100. With what speed should a vehicle move on the turn so that the normal contact force is able to provide the necessary centripetal force?
View SolutionA circular road of radius r is banked for a speed v=40 km/hr. A car of mass m attempts to go on the circular road. The friction coefficient between the tire and the road is negligible.
View SolutionA turn of radius 20 m is banked for the vehicles going at a speed of 36km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
View SolutionTurning Of Vehicle On Frictional Circular Road
View SolutionTurning Of Vehicle On Banked And Frictional Circular Road
View SolutionA circular road of radius 50m has the angle of banking equal to 30^(@) . At what should a vehicle go on this road so that the friction is not used?
View SolutionA smooth circular rod of radius r is banked for a speed v=40km/hr. A car of mass m attempts to go on the circular road. The friction coefficient between the type and the road is negligible, The correct statements are :
View SolutionThe maximum safe speed for which a banked road is intended , is to be increased by 20%. IF the angle of banking is not changed , then the radius of curvature of the road should be changed from the 30 m to
View Solutionसमतल वृत्तीय सड़क पर वाहन की अधिकतम चाल …………….. होनी चाहिए ।
View SolutionA curved road of diameter 1.8 km is banked so that no friction is required at a speed of 30 ms ^(-1) . What is the banking angle ?
View SolutionWhy are circular roads banked? Deduce an expression for maximum speed of a vehicle which can be achieved while taking a turn on the banked curved road neglecting friction.
View Solution

