A straight of length L extends from x=a to x=L+a. the gravitational force it exerts on a point mass 'm' at x=0, if the mass per unit length of the rod is A+Bx2, is given by :
Gm[A(1a+L−1a)−BL]
Gm[A(1a−1a+L)−BL]
Gm[A(1a+L−1a)+BL]
Gm[A(1a−1a+L)−BL]
The correct Answer is:B
dm=rdx=(A+Bx2)dx
F=∫a+LaGmDMx2=GM∫a+La(A+Bx2)dxx2
=GM[∫a+LaAx2dx+a∫a+LaBdx]
F=4m[A(1a−1a+L)]+BL =GM[A(La(a+l))+Bl]

Topper's Solved these Questions
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) SINGLE OPTION CORRECT
Explore 14 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) MULTIPLE OPTIONS CORRECT TYPE
Explore 5 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:Level-2
Explore 30 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 109 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
Similar Questions
If the radius of the earth were to shrink by one per cent, its mass remaining the same, the accleration due to gravity on the earth's surface would
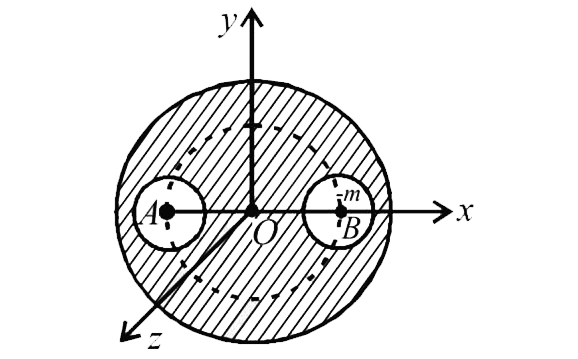
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
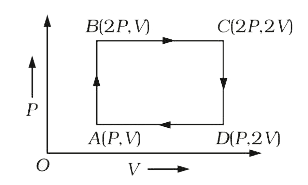
View SolutionAn ideal gas is taken around the cycle ABCDA as shown in the P-V diagram. What is the work done during the cycle?
View SolutionA block of mass 2 kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA rod of length L is placed along the X-axis between x=0andx=L. The linear density (mass/length) ρ of the rod varies with the distance x from the origin as ρj=a+bx. a. Find the SI units of a and b. b. Find the mass of the rod in terms of a,b, and L.
View SolutionA straight rod of length L has one of its end at the origin and the other at X=L . If the mass per unit length of the rod is given by Ax where A is constant, where is its centre of mass?
View SolutionA straight rod of length L extends from x=a to x=L+a . Find the gravitational force exerts on a point mass m at x=0 is (if the linear density of rod mu=A+Bx^(2) )
View SolutionCalculate the force exerted by point mass m on rod of uniformly distributed mass M and length l (Placed as shown in figure)
 .
.
View SolutionA straight of length L extends from x=a to x=L+a. the gravitational force it exerts on a point mass 'm' at x=0, if the mass per unit length of the rod is A+Bx2, is given by :
View SolutionThe mass per unit length of a non- uniform rod OP of length L varies as m=k(x)/(L) where k is a constant and x is the distance of any point on the rod from end 0 .The distance of the centre of mass of the rod from end 0 is
View SolutionA non -uniform rod of length l having mass density lamda(x) = (A+Bx^2) is placed - x - axis with its ends at , (a,0) and (a+ l, 0) . The force it would exert on a point mass m kept at the origin is
View Solutionलम्बाई L की एक छड़ x=a तथा x=L+a के मध्य रखी है। यदि इस छड़ का प्रति इकाई लम्बाई द्रव्यमान A+Bx2 है, तो x=0 पर रखे हुए एक बिन्दु द्रव्यमान m पर, छड़ द्वारा लगाया गुरुत्वीय बल होगा
View SolutionA straight rod of length 'l' extends from x=l to x=2l. If linear mass density of rod is mu=((mu_0)/(l^3)X^3) , then the gravitational force exerted by rod on a particle of mass m at x=0 , is
View SolutionA rod of length L is placed along the X-axis between x=0andx=L. The linear density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx. a.) Find the SI units of a and b b.) Find the mass of the rod in terms of a,b, and L.
View SolutionA straight of length L extends from x=a to x=L+a. the gravitational force it exerts on a point mass 'm' at x=0, if the mass per unit length of the rod is A+Bx^(2), is given by :
View Solution
