A small spherical monoatomic ideal gas bubble (γ=5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure P0 (Neglect surface tension).
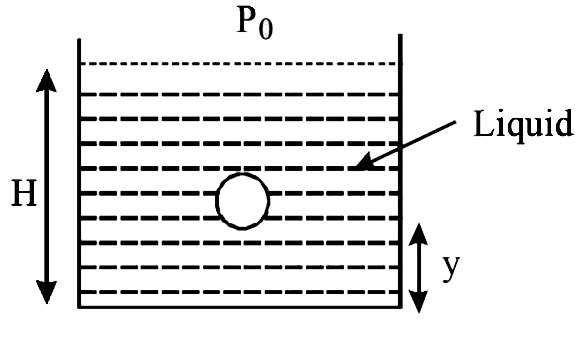
As the bubble moves upwards, besides the buoyancy force the following forces are acting on it
ρlnRgT0P0+ρlgH^(2/5)(P0+ρlgy)7/5
ρlnRgT0(P0+ρlgH)2/5[(P0+ρl(H−Y))]3/5
ρlnRgT0(P0+ρlgH)3/5(P0+ρlgy)8/5
ρlnRgT0(P0+ρlgH)3/5[P0+ρlg(H−Y)]2/5
The correct Answer is:B
FB=ρ1g (Volume of bubble)
Volume can be calculated by
PVγ = Const
(P0+ρ1g(H−Y)P0+ρ1gH)(VV0)5/3=1 ⇒ V=V0(P0+ρ1gHP0+ρ1g(H−y))3/5
So, FB=nRT0ρ1g(P0+ρ1gH)2/5(P0+ρ1g(H−Y))3/5
Topper's Solved these Questions
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE MAIN (ARCHIVE )
Explore 81 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
Explore 1 Video
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) TRUE/FALSE
Explore 1 Video
Similar Questions
A small spherical monoatomic ideal gas bubble (γ=5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure P0 (Neglect surface tension).

When the gas bubble is at a height y from the bottom, its temperature is-
View SolutionA small spherical monoatomic ideal gas bubble (γ=5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure P0 (Neglect surface tension).
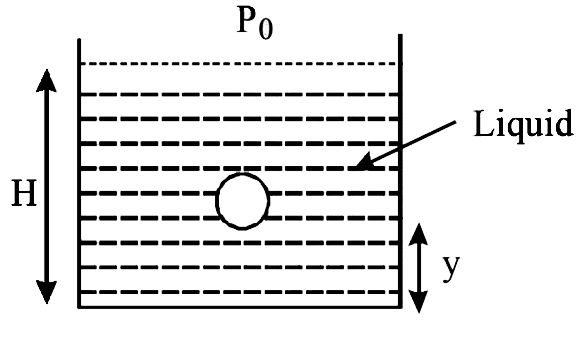
The buoyancy force acting on the gas bubble is (Assume R is the universal gas constant)
View Solution
Knowledge Check
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρWhen a large bubble rises from the bottom of a lake to the surface, its radius doubles, The atmospheric pressure is equal to that of a column of water of height H. The depth of the lake is
AHB2 HC7 HD8 HThe pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depth
A small spherical monoatomic ideal gas bubble (γ=53) is trapped inside a liquid of density ρl (see figure) . Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure is P0 (Neglect surface tension).
_E01_434_Q01.png)
When the gas bubble is at a height y from the bottom , its temperature is :-
View SolutionThe excess pressure inside a soap bubble is
View SolutionA metal sphere connected by a string is dipped in a liquid of density ρ as shown in figure. The pressure at the bottom of the vessel will be, (p0=atmospheric pressure )

View SolutionIf liquid of density ρ is filled in an open cylindrical container to height h, then pressure at bottom
View SolutionThe gas inside a spherical bubble expands uniformly and slowly so that its radius increases from R to 2R. Let the atmospheric pressure be p0 and surface tension be S. The work done by the gas in the process is
View Solution
