One end of an ideal spring is fixed to a wall at origin O and axis of spring is parallel to x-axis. A block of mass m=1kg is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is x=10+3sin(10t). Here, t is in second and x in cm. Another block of mass M=3kg, moving towards the origin with velocity 30cm/s collides with the block performing SHM at t=0 and gets stuck to it. Calculate
(a) new amplitude of oscillations,
(b) new equation for position of the combined body,
( c) loss of energy during collision. Neglect friction.
20 rad/s
5 rad/s
100rad/s
50rad/s
The correct Answer is:B
To solve the problem step by step, we will break down the calculations for each part of the question.
Given Data:
- Mass of block m=1kg
- Mass of block M=3kg
- Initial position equation of the block performing SHM:
x=10+3sin(10t)(in cm)
- Velocity of block M before collision: vM=30cm/s=0.3m/s
Part (a): New Amplitude of Oscillations
1. Calculate the initial momentum before the collision:
- The momentum of block m (1 kg) at t=0:
vm=dxdt=3⋅10cos(10⋅0)=30cm/s=0.3m/s
- The momentum of block M (3 kg):
pM=M⋅vM=3⋅0.3=0.9kg m/s
- Total initial momentum:
pinitial=pm+pM=(1⋅0.3)+(3⋅(−0.3))=0.3−0.9=−0.6kg m/s
2. Calculate the final velocity after the collision using conservation of momentum:
- Let the final velocity of the combined mass be v:
(m+M)v=pinitial⟹(1+3)v=−0.6⟹4v=−0.6⟹v=−0.15m/s
3. Calculate the new amplitude using conservation of energy:
- Initial kinetic energy of the system:
KEinitial=12mv2m+12Mv2M=12⋅1⋅(0.3)2+12⋅3⋅(0.3)2
=12⋅1⋅0.09+12⋅3⋅0.09=0.045+0.135=0.18J
- The spring constant k can be calculated from the SHM equation:
ω=10rad/s⟹k=mω2=1⋅102=100N/m
- The potential energy in the spring at maximum amplitude A:
KEfinal=12kA2
Setting KEinitial=KEfinal:
0.18=12⋅100⋅A2⟹0.18=50A2⟹A2=0.1850=0.0036⟹A=0.06m=6cm
Part (b): New Equation for Position of the Combined Body
1. Calculate the new angular frequency ω′:
- The new mass is 4kg:
ω′=√km+M=√1004=√25=5rad/s
2. Write the new equation of motion:
- The new equation of position will be:
x=10+6sin(5t)(in cm)
Part (c): Loss of Energy During Collision
1. Calculate the energy before and after the collision:
- Initial total energy before collision:
Einitial=KEinitial=0.18J
- Final total energy after collision (using new amplitude):
Efinal=12kA2=12⋅100⋅(0.06)2=0.18J
2. Calculate the loss of energy:
- Since both energies are equal, the loss of energy during the collision is:
Loss of Energy=Einitial−Efinal=0.18−0.18=0J
Summary of Results:
- (a) New amplitude of oscillations: 6cm
- (b) New equation for position: x=10+6sin(5t)
- (c) Loss of energy during collision: 0J
- Mass of block m=1kg
- Mass of block M=3kg
- Initial position equation of the block performing SHM:
x=10+3sin(10t)(in cm)
- Velocity of block M before collision: vM=30cm/s=0.3m/s
- The momentum of block m (1 kg) at t=0:
vm=dxdt=3⋅10cos(10⋅0)=30cm/s=0.3m/s
- The momentum of block M (3 kg):
pM=M⋅vM=3⋅0.3=0.9kg m/s
- Total initial momentum:
pinitial=pm+pM=(1⋅0.3)+(3⋅(−0.3))=0.3−0.9=−0.6kg m/s
- Let the final velocity of the combined mass be v:
(m+M)v=pinitial⟹(1+3)v=−0.6⟹4v=−0.6⟹v=−0.15m/s
- Initial kinetic energy of the system:
KEinitial=12mv2m+12Mv2M=12⋅1⋅(0.3)2+12⋅3⋅(0.3)2
=12⋅1⋅0.09+12⋅3⋅0.09=0.045+0.135=0.18J
- The spring constant k can be calculated from the SHM equation:
ω=10rad/s⟹k=mω2=1⋅102=100N/m
- The potential energy in the spring at maximum amplitude A:
KEfinal=12kA2
Setting KEinitial=KEfinal:
0.18=12⋅100⋅A2⟹0.18=50A2⟹A2=0.1850=0.0036⟹A=0.06m=6cm
- The new mass is 4kg:
ω′=√km+M=√1004=√25=5rad/s
- The new equation of position will be:
x=10+6sin(5t)(in cm)
- Initial total energy before collision:
Einitial=KEinitial=0.18J
- Final total energy after collision (using new amplitude):
Efinal=12kA2=12⋅100⋅(0.06)2=0.18J
- Since both energies are equal, the loss of energy during the collision is:
Loss of Energy=Einitial−Efinal=0.18−0.18=0J
- (a) New amplitude of oscillations: 6cm
- (b) New equation for position: x=10+6sin(5t)
- (c) Loss of energy during collision: 0J
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL (2)
40 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question
56 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 LONG ANSWER TYPE
2 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
A particle stars SHM at time t=0. Its amplitude is A and angular frequency is ω. At time t=0 its kinetic energy is E4. Assuming potential energy to be zero and the particle can be written as (E=total mechanical energy of oscillation).
View SolutionIf a spring has time period T, and is cut into (n) equal parts, then the time period of each part will be.
View SolutionThe phase difference between displacement and acceleration of particle in a simple harmonic motion is
View SolutionA triangular platge of uniform thickness and densilty ismade to rotate about an axis perpendicular to the plane of the paper an a. passing through A b. passing through B, by the application of some foce F at C (mid point of AB) as show in figure. In which case is angular acceleration more?

View SolutionA ball of radius 11 cm and mass 8 kg rolls from rest down a ramp of length 2m. The ramp is inclined at 35° to the horizontal. When the ball reaches the bottom, its velocity is (sin 35° = 0.57)?
View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards abnother block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 The spring constant of the spring fixed at one end is 10 N/m. Find the maximum compression of the spring.
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is mu then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionOne end of an ideal spring is fixed to a wall at origin O and axis of spring is parallel to x-axis. A block of mass m = 1kg is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is x = 10 + 3 sin (10t) . Here, t is in second and x in cm . Another block of mass M = 3kg , moving towards the origin with velocity 30 cm//s collides with the block performing SHM at t = 0 and gets stuck to it. Calculate (a) new amplitude of oscillations, (b) neweqution for position of the combined body, ( c) loss of energy during collision. Neglect friction.
View SolutionA block of mass m is dropped onto a spring of constant k from a height h . The second end of the spring is attached to a second block of mass M as shown in figure. Find the minimum value of h so that the block M bounces off the ground. If the block of mass m sticks to the spring immediately after it comes into contact with it.
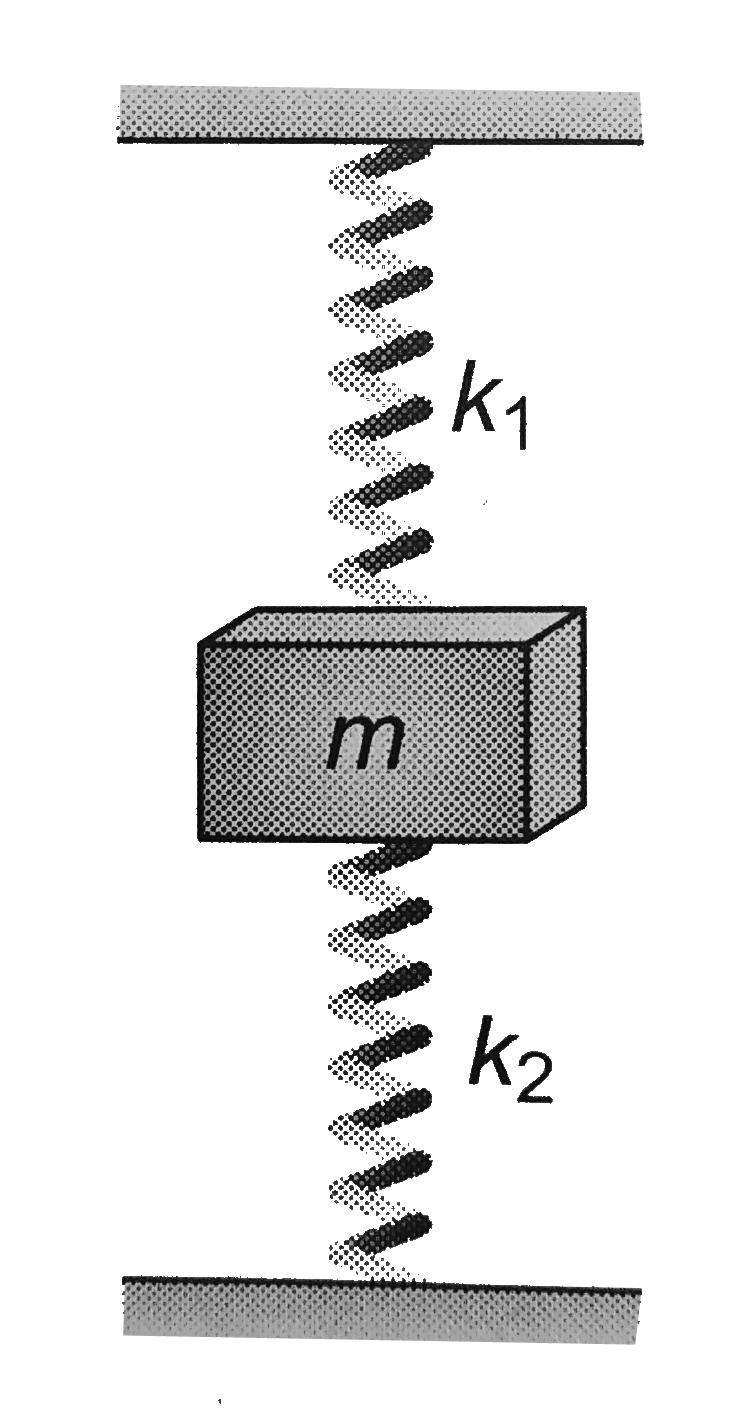
View SolutionIn the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
View SolutionA block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant k) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched (x=0). When a constant horizontal force →F in the positive direction of the x−axis is applied to it, a plot of the resulting kinetic energy of the block versus its position x is shown in figure. What is the magnitude of →F ?
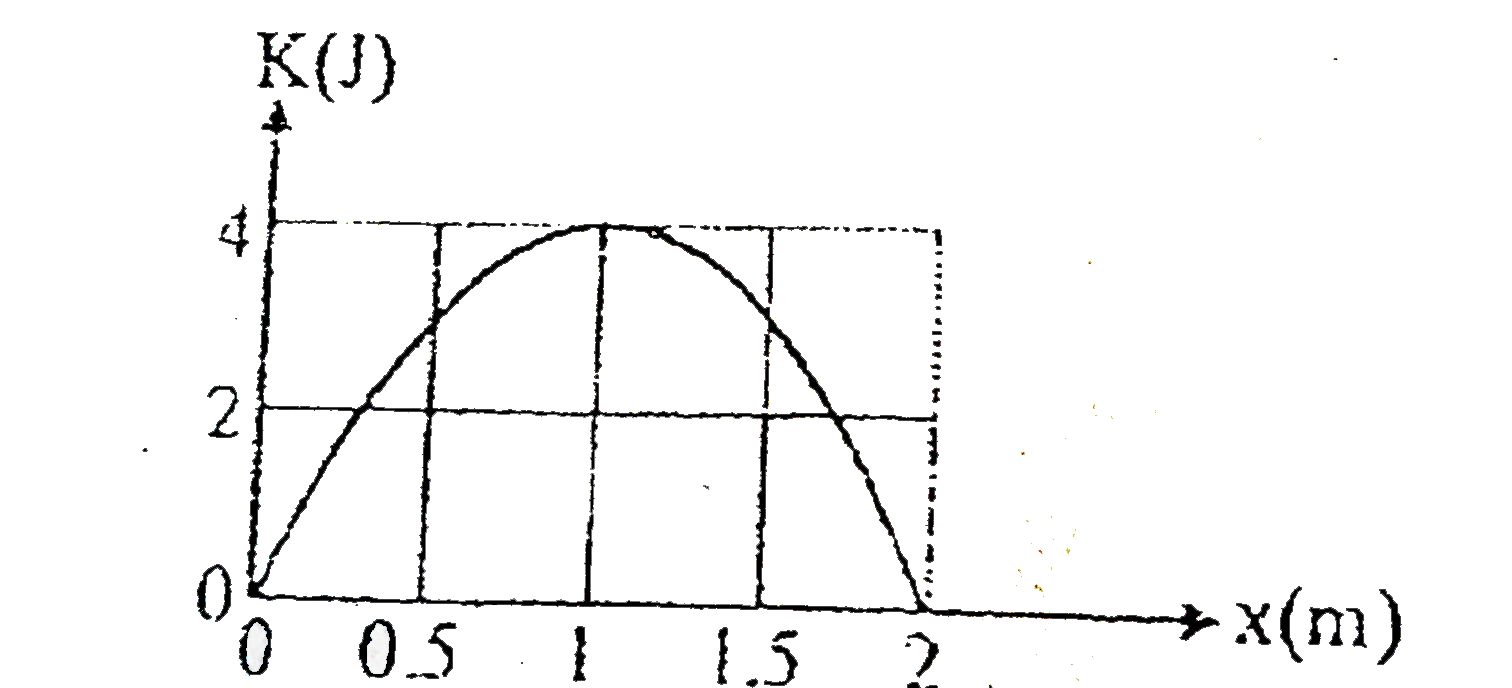
View SolutionA block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant k) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched (x=0). When a costant horizontal force →F in the positive direction of the x−axis is applied to it, a plot of the resulting kinetic energy of the block verus its position x is shown in figure. What is the magnitude of →F
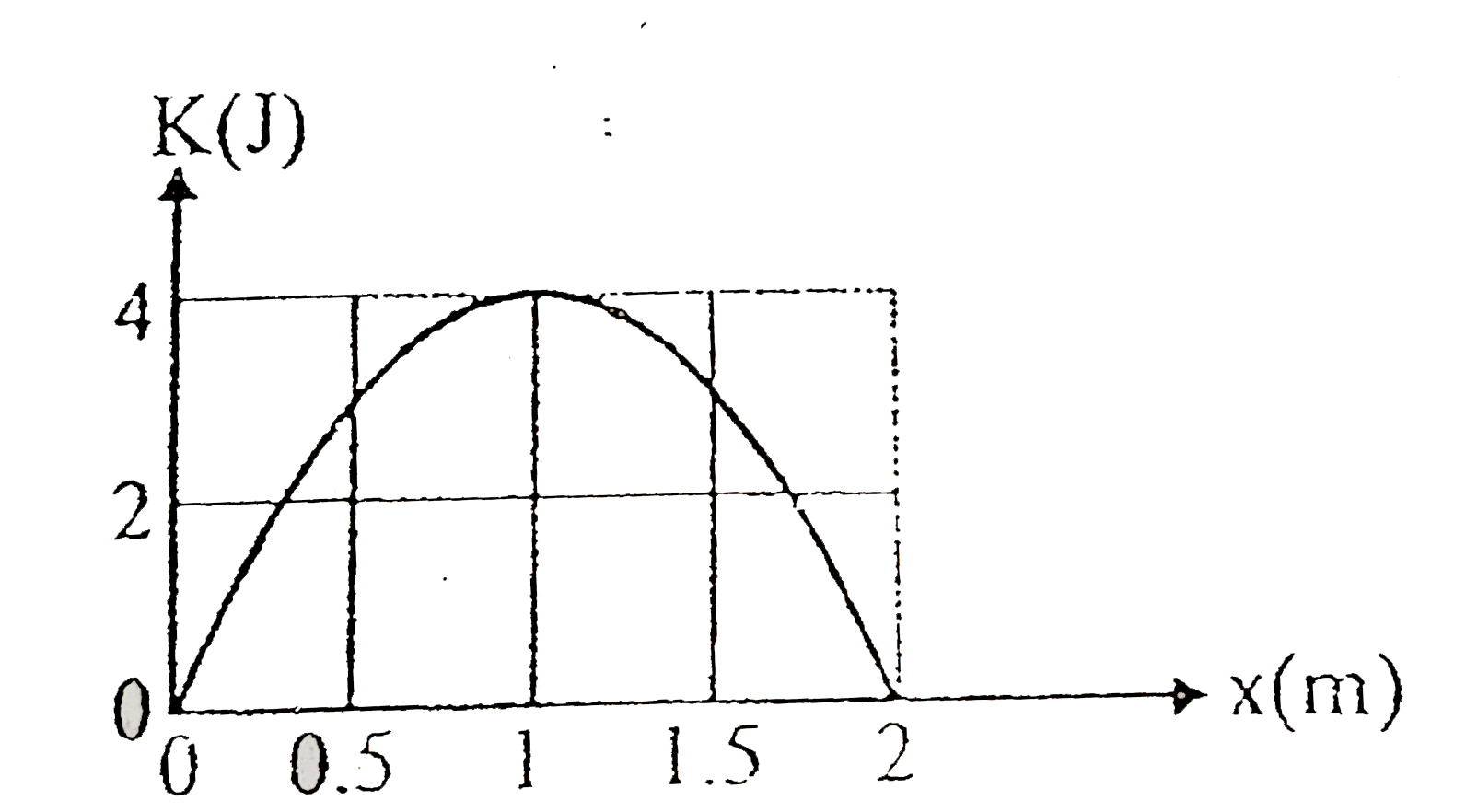
View SolutionA block of mass m=1kg is attached to a free end of a spring whose one end is fixed with as shown in the figure. The block is performing simple harmonic motion. The position of the block from O is given by x=2+(1)/(sqrt(2))sin2t , where x is in meter and t is in second. A particle of same mass is released from the circular path at a height h=80cm . then particle collidic and stricks to the block. The collision takes place when velocity of the block is zero and spring is elongated. Find ( i ) Time period of new SHM . ( ii ) Maximum velocity of the system
View SolutionA spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
View SolutionA mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
View Solution

