Can a single isolated particle possess potential energy? Justify.
To determine whether a single isolated particle can possess potential energy, we need to analyze the concept of potential energy in relation to forces and systems of particles.
1. Definition of Potential Energy:
Potential energy is the energy stored in an object due to its position relative to other objects. It is often associated with the gravitational force, elastic force, or electric force acting between two or more objects.
2. Isolated Particle:
An isolated particle is one that does not interact with any other particles or forces. It exists independently in space without any external influence.
3. Conditions for Potential Energy:
For an object to have potential energy, there must be a force acting on it due to another object. This interaction creates a potential energy associated with the position of the object within a field (like gravitational or electric fields).
4. Example of a System:
Consider a system consisting of two masses, such as Earth and Mars. The gravitational force between them creates a potential energy in the system. The potential energy depends on their positions relative to each other.
5. Conclusion for a Single Particle:
Since a single isolated particle does not interact with any other particle or force, it does not have a reference point to measure potential energy against. Therefore, it cannot possess potential energy by itself.
6. Final Justification:
Potential energy is a property of a system of particles rather than an individual particle. Thus, a single isolated particle cannot possess potential energy.
Final Answer:
No, a single isolated particle cannot possess potential energy because potential energy is defined in the context of interactions between particles or systems of particles.
---
Potential energy is the energy stored in an object due to its position relative to other objects. It is often associated with the gravitational force, elastic force, or electric force acting between two or more objects.
An isolated particle is one that does not interact with any other particles or forces. It exists independently in space without any external influence.
For an object to have potential energy, there must be a force acting on it due to another object. This interaction creates a potential energy associated with the position of the object within a field (like gravitational or electric fields).
Consider a system consisting of two masses, such as Earth and Mars. The gravitational force between them creates a potential energy in the system. The potential energy depends on their positions relative to each other.
Since a single isolated particle does not interact with any other particle or force, it does not have a reference point to measure potential energy against. Therefore, it cannot possess potential energy by itself.
Potential energy is a property of a system of particles rather than an individual particle. Thus, a single isolated particle cannot possess potential energy.
No, a single isolated particle cannot possess potential energy because potential energy is defined in the context of interactions between particles or systems of particles.
টপার এই প্রশ্নগুলো সমাধান করেছে
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 0 - LONG ANSWER TYPE
5 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - Level - 1
87 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Video
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
109 Videos
সম্পর্কিত প্রশ্ন
Define mechanical energy and law of conservation of mechanical energy. Prove conversion of gravitational potential energy in to kinetic energy by the help of law of conservation of mechanical energy. Also draw graph between energy and height.
View SolutionA particle moves 5m in the +x direction while being acted upon by a constant force→F=(4N)ˆi+(2N)ˆj−(4N)ˆk . The work done on the particle by this force is
View SolutionTwo particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m/s, their centre of mass has a velocity of 0.5 m/s. When the relative velocity of approach becomes 3m/s, the velocity of the centre of mass is 0.75 m/s.
View SolutionA hollow metal sphere of radius 5 cm is charged so that the potential on its surface is 10 V. The potential at the centre of the sphere is
View SolutionAn ideal gas is taken around the cycle ABCDA as shown in the P-V diagram. What is the work done during the cycle?
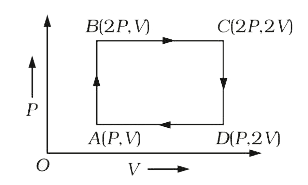
View SolutionThe gravitational potential energy of an isolated system of three particles, each of mass m, at the three corners of an equilateral triangle of side l is
View SolutionCan a single isolated force exist in nature ?
View SolutionWhy is it not possible to measure the single electrode potential ?
View SolutionIs potential energy the property of a single object? Justify.
View SolutionCan a single isolated particle possess potential energy? Justify.
View SolutionIs potential energy the property of a single object? Justify.
View SolutionIs potential energy the property of a single object? Justify.
View SolutionCan you explain the translation of a car by the translation of a single particle? Justify your answer.
View SolutionElastic potential energy possessed by a spring is
View Solution(A) : A body can possess mechanical energy without momentum.
(R ) : A bent bow potential energy by virtue of deformation.
View Solution

