The direct conversion of A or B is difficult, hence it is carried out by the following shown path
Given, ΔSA→C=50eu, ΔSC→D=30eu,ΔSB→D=20eu
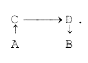
Where eu is entropy unit, then ΔSA→B is .
+100 eu
+60 eu
−100 eu
−60 eu
The correct Answer is:B
C↓A→D↓B
Given, ΔSA→C=50eu
ΔSC→D=30eu,ΔSB→D=20eu
Where, eu is entropy unit
Therefore, ΔSA→C+ΔSC→D−ΔSB→D=50+30−20=60 eu
टॉपर्स ने हल किए ये सवाल
- THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:THERMODYNAMICSExercise:LEVEL-2 (NUMERICAL VALUE TYPE)
Explore 15 Videos
- THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:THERMODYNAMICSExercise:JEE (MAIN ARCHIVE)
Explore 32 Videos
- THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:THERMODYNAMICSExercise:LEVEL-1
Explore 74 Videos
- THERMOCHEMISTRYBook:VMC MODULES ENGLISHChapter:THERMOCHEMISTRYExercise:JEE ADVANCED (ARCHIVE)
Explore 31 Videos
- THERMODYNAMICS & THERMOCHEMISTRYBook:VMC MODULES ENGLISHChapter:THERMODYNAMICS & THERMOCHEMISTRYExercise:Impeccable
Explore 48 Videos
समान प्रश्न
The direct conversion of A to B is difficult, hence it is carried out as
A→C→D→B
Given, ΔS(A→C)=50eU,ΔS(C→D)=30eU,ΔS(B→D)=20eU, where eU is entropy unit. Thus the change in entropy in (A→B) is:
View SolutionThe direct conversion of A to B is difficult, hence it is carried out as
A→C→D→B
Given, ΔS(A→C)=50eU,ΔS(C→D)=30eU,ΔS(B→D)=20eU, where eU is entropy unit. Thus the change in entropy in (A→B) is:
View Solutiona process A rarr D is difficult to occur directly instead it takes place in three successive steps, DeltaS(ArarrB)=40 e.u., DeltaS(BrarrC)=30 e.u., DeltaS(DrarrC)=20 e.u. where e.u. is entropy unit then the entropy change DeltaS for the process (ArarrD) is
View SolutionIf ABC is an isosceles triangle and D is a point on BC such that AD⊥BC then,
View SolutionA triangle ABC is an isosceles triangle if any one of the following conditions hold: (a) Altitude AD bisects ∠BAC (b) Bisector of ∠BAC is perpendicular to the base BC.
View SolutionA triangle ABC is an isosceles triangle if any one of the following conditions hold: Altitude AD bisects ∠BAC Bisector of ∠BAC is perpendicular to the base BC
View SolutionIn a ΔABC,b=12 units, c = 5 units and Δ=30sq. units. If d is the distance between vertex A and incentre of the triangle then the value of d2 is _____
View SolutionΔCDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
View SolutionIf ΔABC~ΔDEF such that BC=3cm , EF=4cm and ar(ABC)=54cm2 , then ar(DEF)=
View SolutionIn the given figure, ΔABC,AB=3cm,BC=4cm and AC=5cm. Name the smallest and the largest angles of the triangle.
View Solution
