The acceleration of a particle is increasing linerly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
v0t+13bt2
v0t+13bt3
v0t+16bt3
v0+12bt2
The correct Answer is:C
Step by step video solution for The acceleration of a particle is increasing linerly with time t as bt. The particle starts from the origin with an initial velocity v_(0). The distance travelled by the particle in time t will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE & PLANE Book:VMC MODULES ENGLISHChapter:MOTION IN A STRAIGHT LINE & PLANE Exercise:EFFICIENT
Explore 50 Videos
- MOCK TEST 9Book:VMC MODULES ENGLISHChapter:MOCK TEST 9Exercise:PHYSICS (SECTION 2)
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
Similar Questions
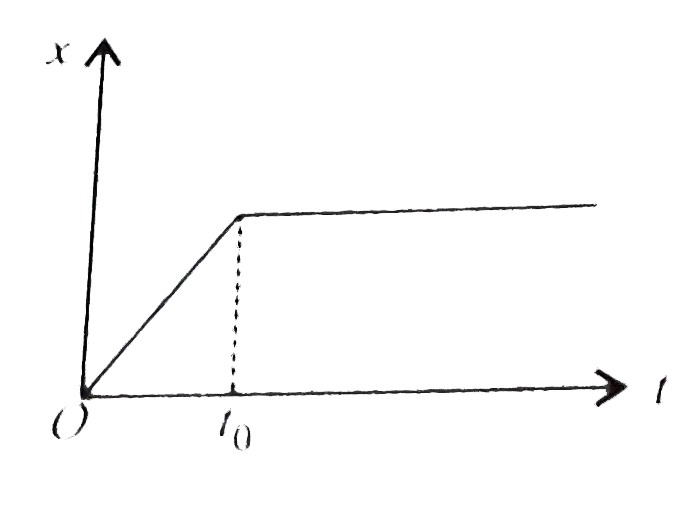
Figure shows the displacement (x)- time (t) graph of the particle moving on the axis.
View SolutionA carnot engine operates with source at 127∘C and sink at 27∘C. If the source supplies 40kJ of heat energy. The work done by the engine is
View SolutionA particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v_0 . The distance travelled by the particle in time t will be
View SolutionThe acceleration of particle is increasing linearly with time t as bt . The particle starts from the origin with an initial velocity v_0 . The distance travelled by the particle in time t will be.
View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin ( pit ), where t is in seconds and a is in m/ s^2 . The initial velocity of particle (at time t = 0) is u = 0. Q. Then the distance travelled (in meters) by the particle from time t = 0 to t = t will be :
View SolutionThe acceleratin of a particle increases linearly with time t as 6t. If the initial velocity of the particles is zero and the particle starts from the origin, then the distance traveled by the particle in time t will be
View Solutionएक कण का त्वरत t के प्रति रेखीयता bt के अनुसार बढ़ता है |कण मूल बिन्दु से प्रारम्भिक v0 वेग से चलता है । t समय के कण द्वारा तय की गई दूरी होगी
View SolutionThe acceleration of a particle increasing linearly with timer is be. The particle starts from the origin with an initial velocity, The distance travelled by the particle in time will be
View SolutionThe acceleration of a particle increasing linearly with timer is be. The particle starts from the origin with an initial velocity, The distance travelled by the particle in time will be
View SolutionThe acceleration of a particle increasing linearly with timer is be. The particle starts from the origin with an initial velocity, The distance travelled by the particle in time will be
View Solutionयदि किसी कण का प्रारम्भिक वेग u है तथा इसी दिशा मे त्वरण समय के साथ bt अनुसार बदलता है तो कण का किसी क्षण t पर वेग क्या होगा?
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v_0 . The distance travelled by the particle in time t will be
View SolutionThe acceleration of a particle is increasing linearly with time t as bt.The particle starts from origin with an initial velocity V_(0) .The distance travelled by the particle in time t will be
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from origin with an initial velocity v_(0) . The distance travelled by the particle in time t will be
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0 . The distance travelled by the particle in time t will be
View Solution
