Two blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
(a)m1/m2
(b)m2/m1
(c)m1−m2m1+m2
(d)4m1m2(m1+m2)
The correct Answer is:2
To solve the problem of finding the ratio of the accelerations of two blocks connected by a light spring on a horizontal frictionless table, we can follow these steps:
1. Identify the Masses:
Let the mass of the first block be m and the mass of the second block be m′.
2. Understand the System:
When the spring is compressed and then released, both blocks will experience forces due to the spring. According to Newton's third law, the force exerted by the spring on each block will be equal in magnitude and opposite in direction.
3. Apply Newton's Second Law:
For the first block (mass m):
F=m⋅a
where F is the force exerted by the spring on block m and a is the acceleration of block m.
For the second block (mass m′):
F′=m′⋅a′
where F′ is the force exerted by the spring on block m′ and a′ is the acceleration of block m′.
4. Set Forces Equal:
According to Newton's third law, the forces exerted by the spring on both blocks are equal in magnitude:
F=F′
This gives us:
m⋅a=m′⋅a′
5. Rearrange the Equation:
From the equation m⋅a=m′⋅a′, we can express the ratio of the accelerations:
aa′=m′m
6. Final Ratio of Accelerations:
Thus, the ratio of the accelerations of the two masses is:
aa′=m′m
Conclusion:
The ratio of the accelerations of the masses m and m′ is given by:
aa′=m′m
Let the mass of the first block be m and the mass of the second block be m′.
When the spring is compressed and then released, both blocks will experience forces due to the spring. According to Newton's third law, the force exerted by the spring on each block will be equal in magnitude and opposite in direction.
For the first block (mass m):
F=m⋅a
where F is the force exerted by the spring on block m and a is the acceleration of block m.
F′=m′⋅a′
where F′ is the force exerted by the spring on block m′ and a′ is the acceleration of block m′.
According to Newton's third law, the forces exerted by the spring on both blocks are equal in magnitude:
F=F′
This gives us:
m⋅a=m′⋅a′
From the equation m⋅a=m′⋅a′, we can express the ratio of the accelerations:
aa′=m′m
Thus, the ratio of the accelerations of the two masses is:
aa′=m′m
The ratio of the accelerations of the masses m and m′ is given by:
aa′=m′m
Topper's Solved these Questions
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EFFICIENT
50 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
Similar Questions
Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionTwo blocks A and B of masses mA and mB are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Show that the kinetic energies of the blocks are, at any instant inversely proportional to their masses.
View SolutionTwo blocks A and B of masses 1kg and 2kg are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Find the ratio of their,
(a) speed
(b) magnitude of momentum and
(c) kinetic energy at any instant.
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
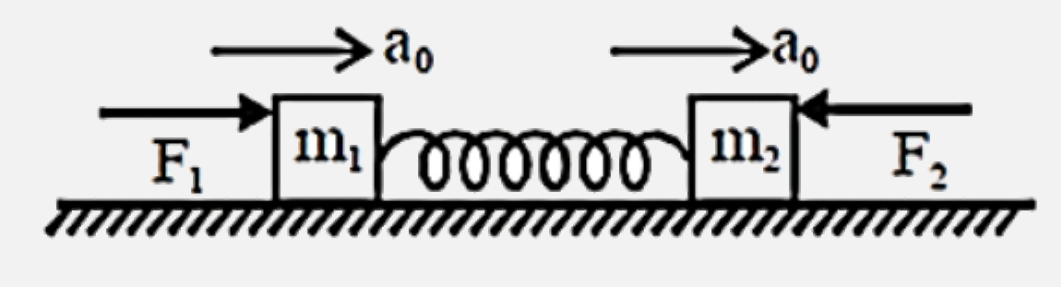
View SolutionTwo blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth plane .find the value of spring force .
View SolutionTwo blocks of masses 6 kg and 3 kg are attached to the two ends of a massless spring of spring constant 2π2N/m. If spring is compressed and released on a smooth horizontal surface then find the time period (in seconds) of each block.
View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .
.
View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .
.
View SolutionTwo blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
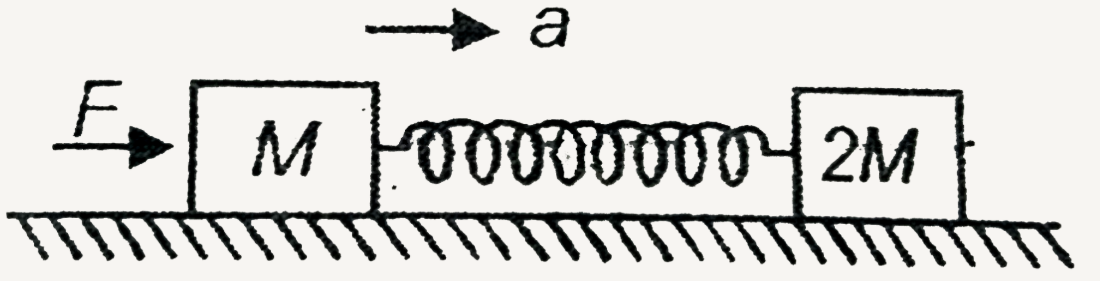
View SolutionTwo blocks of masses M and 2M are connected to each other through a light spring as shown in figure . If we push the mass M with a force F which cause acceleration a in mass M. what will the acceleration in 2M?
View Solution

