A solid sphere rests on a horizontal surface. A horizontal impulse is applied at height h from centre. The sphere starts rolling just after the application of impulse. The ratio h/R will be
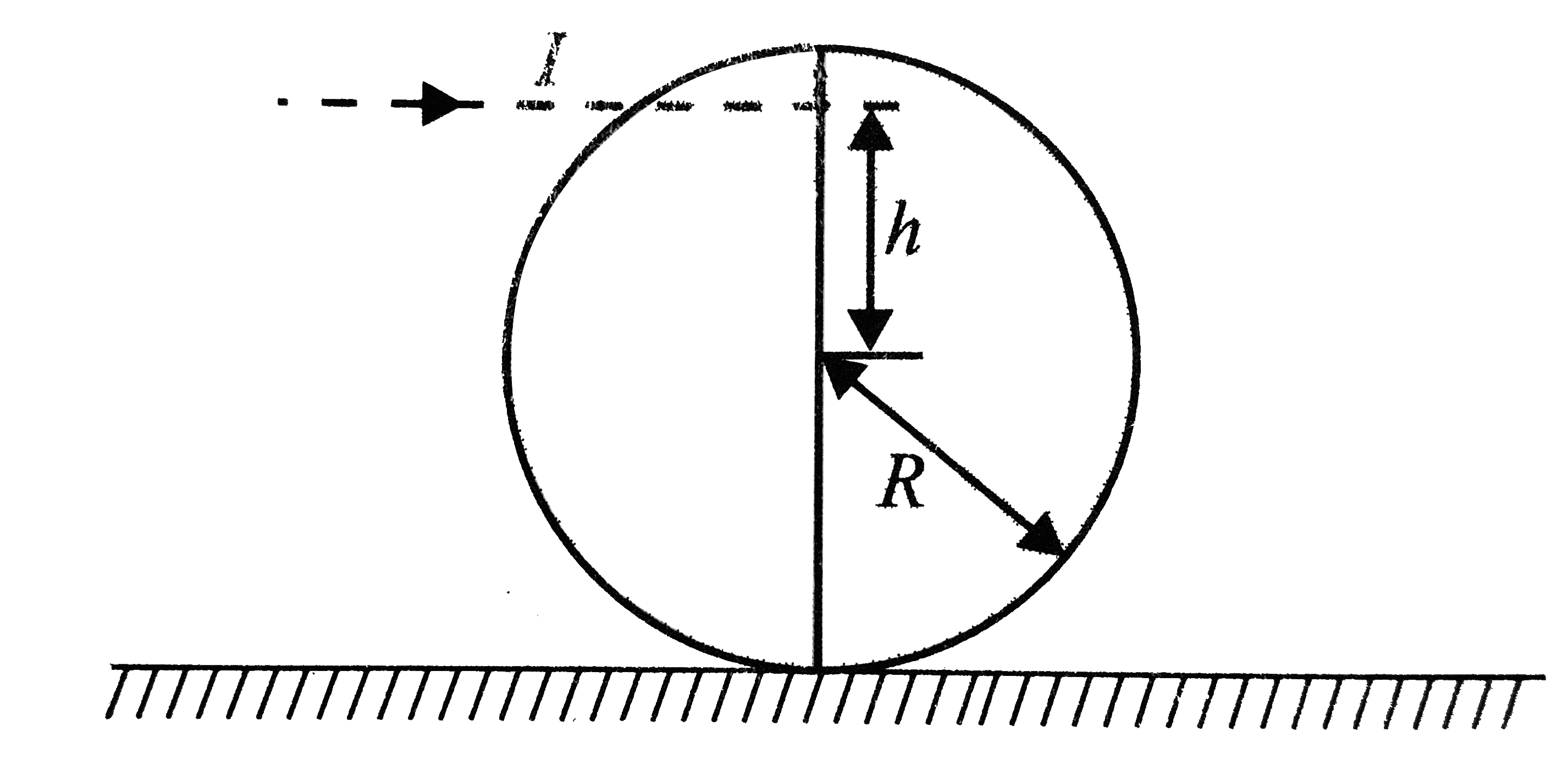
12
25
14
15
The correct Answer is:B
Step by step video solution for A solid sphere rests on a horizontal surface. A horizontal impulse is applied at height h from centre. The sphere starts rolling just after the application of impulse. The ratio h//R will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:EFFICIENT
Explore 50 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:IMPECCABLE
Explore 56 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:IMPECCABLE
Explore 56 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBook:VMC MODULES ENGLISHChapter:SYSTEM OF A PARTICLES & ROTATIONAL MOTIONExercise:IN-CHAPTER EXERCISE F
Explore 10 Videos
- UNITS, MEASUREMENTS & ERRORSBook:VMC MODULES ENGLISHChapter:UNITS, MEASUREMENTS & ERRORSExercise:IN - CHAPTER EXERCISE - B
Explore 10 Videos
Similar Questions
The moment of inertia of a body about a given axis of rotation depends upon :-
View SolutionThe angular momentum of body remains conserve if :
View SolutionThe angular momentum of body remains conserve if :
View SolutionA ball of radius 11 cm and mass 8 kg rolls from rest down a ramp of length 2m. The ramp is inclined at 35° to the horizontal. When the ball reaches the bottom, its velocity is (sin 35° = 0.57)?
View SolutionWhich of the following is dimensionally correct?
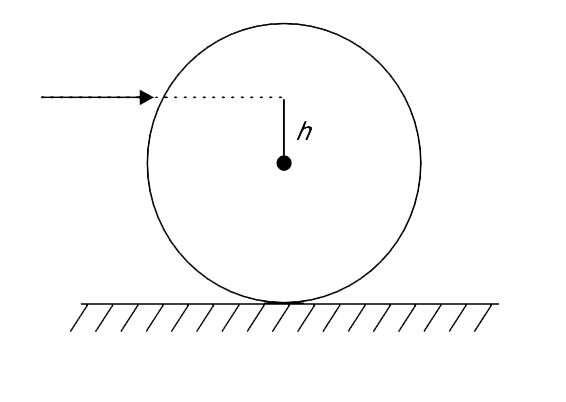
View SolutionA solid sphere rests on a horizontal surface. A horizontal impulse is applied at height h from centre. The sphere starts rolling just after the application of impulse. The ratio h/r will be
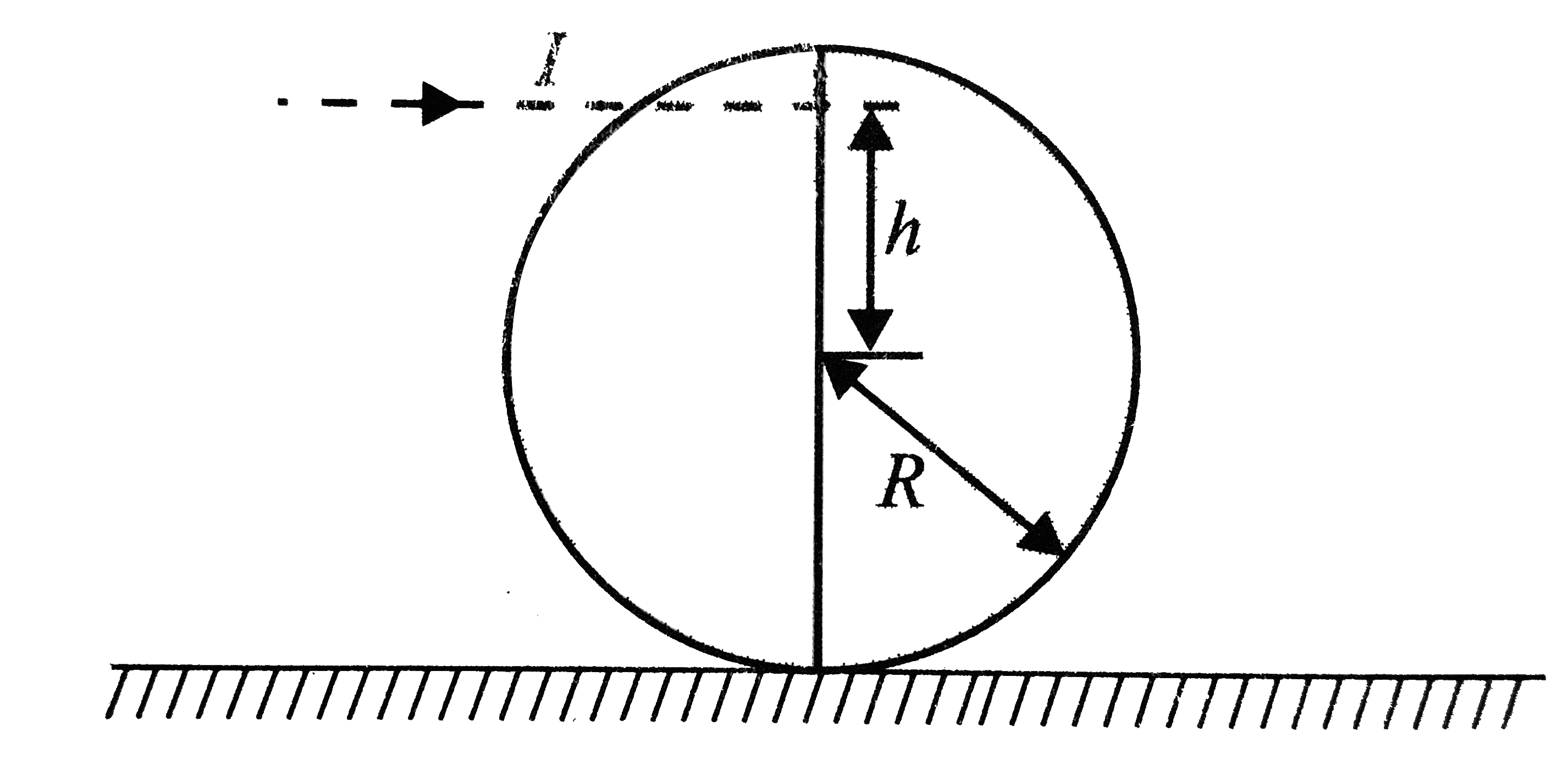
View SolutionA uniform sphere of mass m and radius R is placed on a rough horizontal surface. The spher is struck horizontally at a height h from the floor. Show that the sphere rolls without slipping with a constant velocity, when h=7R/5.
View Solution
A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,
View SolutionA homogeneous solid sphere of radius R is resting on a horizontal surface. It is set in motion by a horizontal impulse imparted to it at a height h above the centre. If h is greater than h0, the velocity of the sphere increases in the direction of its motion after the start. If h<h0 the velocity decreases after the start. Find h0
View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View SolutionA uniform sphere is placed on a smooth horizontal surface and a horizontal force F is applied on it at a distance h above the surface. The acceleration of the centre :
View SolutionA solid sphere of radius R is resting on a smooth horizontal surface. A constant force F is applied at a height h from the bottom. Vhoose the correct alternative.
View Solutionएक एकसमान गोला एक घर्षणरहित क्षैतिज सतह पर रखा हुआ है | सतह से h ऊँचाई के एक बिंदु पर एक क्षैतिज बल F लगाया जाता है | गोले के केंद्र का त्वरण
View SolutionA solid sphere is placed on a horizontal plane. A horizontal impulse I is applied at a distance h above the central line as shown in the figure. Soon after giving the impulse the sphere starts rolling. The ratio (h)/(R) would be
View SolutionA uniform sphere is placed on a smooth horizontal surface and a horzontal force F is applied on it at a distance .h. above the surface. The acceleration of the centre
View SolutionA uniform sphere is placed on a smooth horizontal surface and a horzontal force F is applied on it at a distance .h. above the surface. The acceleration of the centre
View Solution
