An electron (mass =9.0×10−31 kg and charge =1.6×10−19 coulomb) is moving in a circular orbit in a magnetic field of 1.0×10−4weber/m2. Its perido of revolution is
3.5×10−7 second
7.0×10−7 second
1.05×10−6 second
2.1×10−6 second
The correct Answer is:A
To find the period of revolution of an electron moving in a magnetic field, we can use the formula for the time period T of a charged particle moving in a circular path in a magnetic field. The formula is given by:
T=2πmqB
Where:
- T is the period of revolution,
- m is the mass of the electron,
- q is the charge of the electron,
- B is the magnetic field strength.
Step 1: Identify the given values
- Mass of the electron, m=9.0×10−31 kg
- Charge of the electron, q=1.6×10−19 C
- Magnetic field strength, B=1.0×10−4 Wb/m²
Step 2: Substitute the values into the formula
Substituting the values into the formula for the period of revolution:
T=2π(9.0×10−31)(1.6×10−19)(1.0×10−4)
Step 3: Calculate the denominator
First, calculate the denominator:
(1.6×10−19)(1.0×10−4)=1.6×10−23
Step 4: Calculate the numerator
Now calculate the numerator:
2π(9.0×10−31)≈2×3.14×9.0×10−31≈5.654×10−30
Step 5: Calculate the period T
Now, divide the numerator by the denominator:
T=5.654×10−301.6×10−23≈3.53×10−7 seconds
Step 6: Round the answer
Rounding to two significant figures, we get:
T≈3.5×10−7 seconds
Thus, the period of revolution of the electron is approximately 3.5×10−7 seconds.
Final Answer
The period of revolution is 3.5×10−7 seconds.
---
- T is the period of revolution,
- m is the mass of the electron,
- q is the charge of the electron,
- B is the magnetic field strength.
- Mass of the electron, m=9.0×10−31 kg
- Charge of the electron, q=1.6×10−19 C
- Magnetic field strength, B=1.0×10−4 Wb/m²
Substituting the values into the formula for the period of revolution:
First, calculate the denominator:
Now calculate the numerator:
Now, divide the numerator by the denominator:
Rounding to two significant figures, we get:
The period of revolution is 3.5×10−7 seconds.
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:ENABLE
Explore 50 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:EFFICIENT
Explore 50 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:MCQ
Explore 2 Videos
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
Explore 1 Video
Similar Questions
What is the radius of the path of an electron (mass 9×10−31 kg and charge 1.6×10−19C) moving at a speed of 3×107m/s in a magnetic field of 6×10−4T perpendicular to it? What is its frequency? Calculate its energy in keV.(1eV=1.6×10−19J).
View SolutionAn electron (mass =9.1×10−31kg, charge =1.6×10−19C) experiences no deflection if subjected to an electric field of 3.2x105Vm, and a magnetic fields of 2.0×10−3Wbm2. Both the fields are normal to the path of electron and to each other. If the electric field is removed, then the electron will revolve in an orbit of radius
View SolutionAn electron (mass =9.1×10−31kg, charge =1.6×10−19C) experiences no deflection if subjected to an electric field of 3.2x105Vm, and a magnetic fields of 2.0×10−3Wbm2. Both the fields are normal to the path of electron and to each other. If the electric field is removed, then the electron will revolve in an orbit of radius
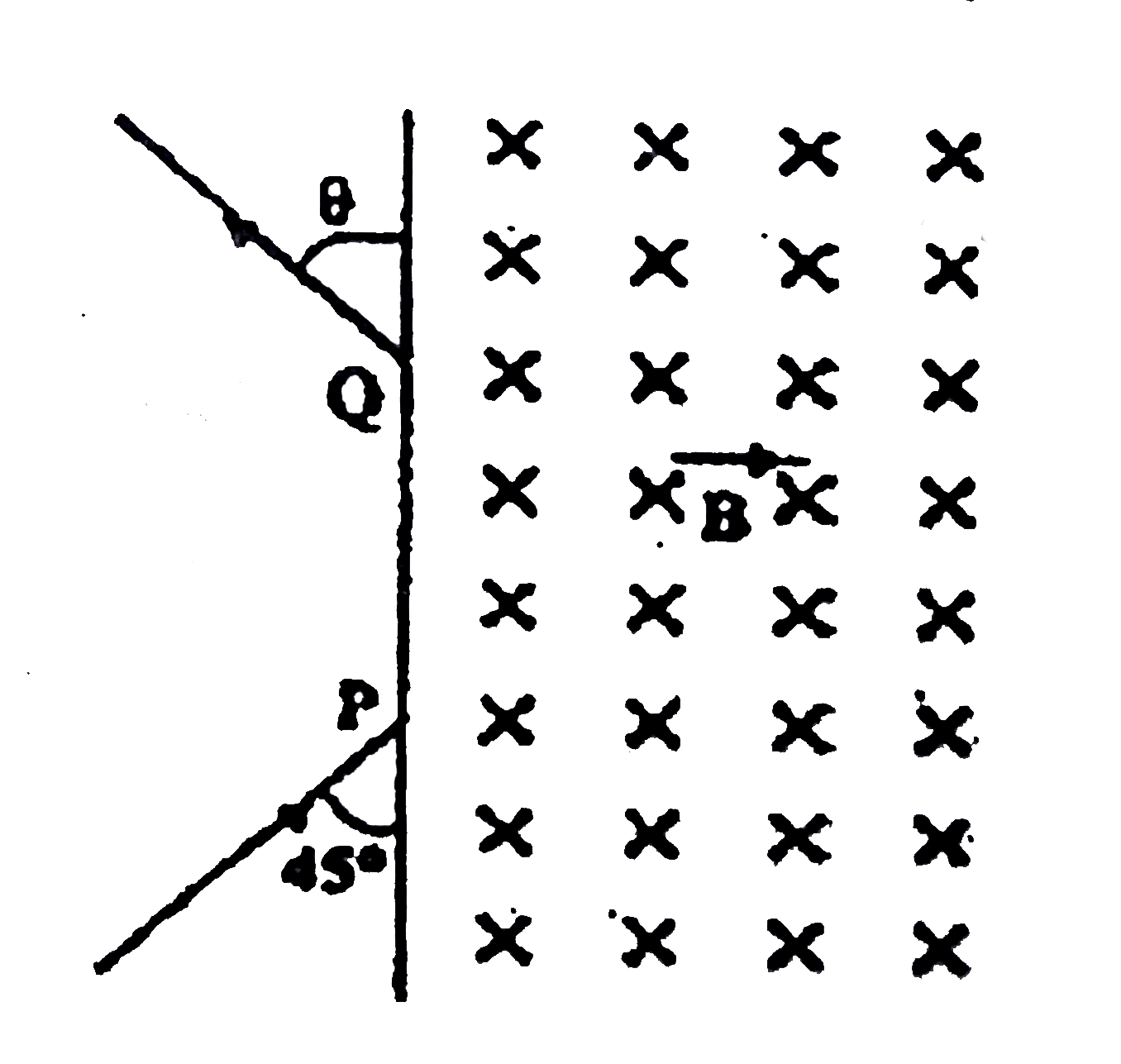
View SolutionA particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
View SolutionA proton of mass 1.67×10−27 kg and charge 1.6×10−19C is shot a uniform magnetic field, and perpendicular to the field with a velocity 5×106m/s. If the magnetic induction of the field is 1 tesla, find
(i) The radius of the circular path
View SolutionAn electron (q=1.6×10−19C) is moving at right angles to a uniform magnetic field of 3.534×10−5 T The time taken by the electron to complete a circular orbit is
View SolutionAn electron having charge 1.6×10−19C and mass 9×10−31 kg is moving with 4×106ms−1 speed in a magnetic field 2×10−1 tesla in circular orbit. The force acting on electron and the radius of the circular orbit will be
View SolutionAn electron is moving in a circular path under the influence fo a transerve magnetic field of 3.57×10−2T. If the value of e/m is 1.76×10141C/kg. The frequency of revolution of the electron is
View SolutionThe mass of an electron is 9.1×10−31 kg and velocity is 2.99×1010cms−1. The wavelenth of the electron will be
View SolutionAn electron of mass 0.90×10−30 kg under the action of a magnetic field moves in a circle of 2.0 cm radius at a speed 3.0×106ms−1. If a proton of mass 1.8×10−27kg was to move in a circle of the same radius in the same magnetic field, then its speed will be
View Solution
