Two similar thin equi-convex lenses, of focal f each, are kept coaxially in contact with each other such that the focal length of the combination is F1, When the space between the two lens is filled with glycerin (which has the same refractive index (μ=1.5) as that of glass) then the equivlent focal length is F2, The ratio F1:F2 will be
2:1
1:2
2:3
3:4
The correct Answer is:B
Step by step video solution for Two similar thin equi-convex lenses, of focal f each, are kept coaxially in contact with each other such that the focal length of the combination is F_(1), When the space between the two lens is filled with glycerin (which has the same refractive index (mu=1.5) as that of glass) then the equivlent focal length is F_(2), The ratio F_(1): F_(2) will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - EFFICIENT
49 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- REVISION TEST-15 JEE - 2020BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-15 JEE - 2020EXERCISE - PHYSICS
25 Videos
Similar Questions
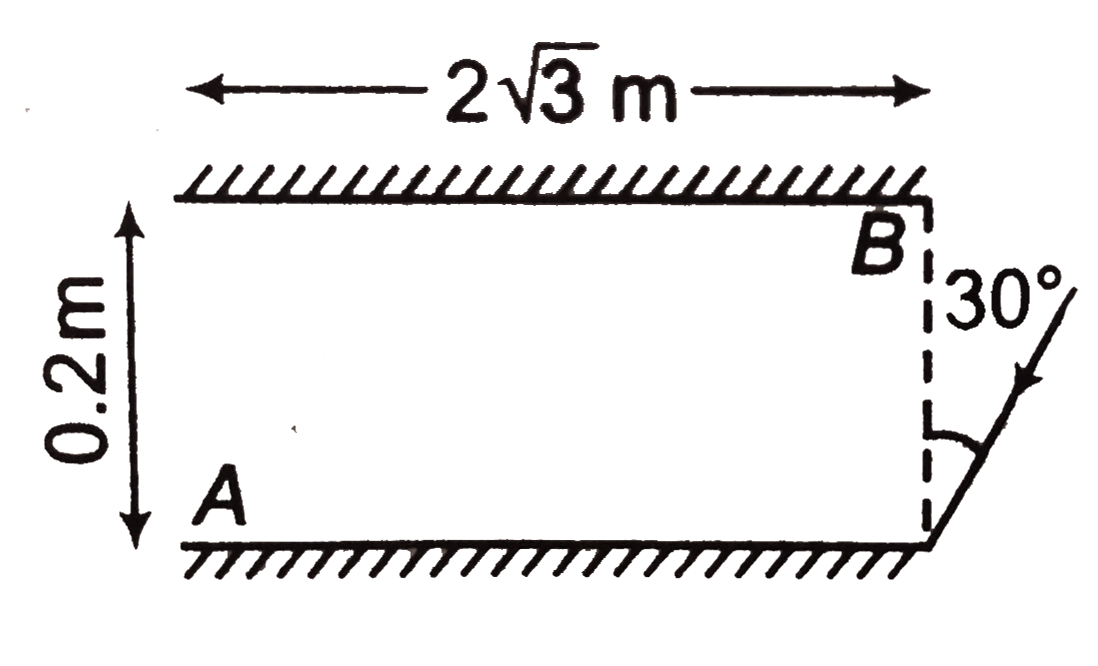
Two plane mirrors A and B are aligned parallel to each other as shown in the figure. A light ray is incident at an angle of 30∘ at a point just inside one end of A. The number of times the ray undergoes reflections (including the first one) before it emerges out is
View SolutionWhich of the following statements is not correct
View SolutionA particle is moving with speed v=b√x along positive x-axis. Calculate the speed of the particle at time t=τ (assume tha the particle is at origin at t= 0).
View SolutionTwo similar thin equi-convex lenses, of focal f each, are kept coaxially in contact with each other such that the focal length of the combination is F1, When the space between the two lens is filled with glycerin (which has the same refractive index (μ=1.5) as that of glass) then the equivalent focal length is F2, The ratio F1:F2 will be
View SolutionTwo thin lenses of focal length f1 and f2 are in contact and coaxial. The power of the combination is
View SolutionTwo thin lenses of focal lengths f_(1) and f_(2) are in contact. The focal length of this combination is
View SolutionDerive the relation : (1)/(F) =(1)/(f_(1)) +(1)/(f_(2)) ,where f_(1) and f_(2) are focal length of two thin lenses and F is the focal length of the combination in contact.
View Solutionf1 और f2 फोकस-दुरी के दो पतले लेंस एक-दूसरे के संपर्क में रखे हुए हैं। यह संयोजन एक ऐसे पतले लेंस जैसा व्यवहार करेगा जिसकी फोकस-दुरी होगी
View SolutionTwo thin convex lenses of focal lengths f1 and f2 are in contact and coaxial. The power of the combination is
View SolutionWhen a number of thin lenses of focal lengths [f_(1),f_(2),f_(3)......" are in contact,then effective focal length is
View SolutionExpress the combined power of two lenses, one of focal length +f1 and of the other −f2 in contact with each other.
View SolutionTwo thin convex lenses of focal lengths f_(1) and f_(2) are arranged coaxially with ‘d’ as the reparation between them. The equivalent lens of the combination with focal length ‘F’ to be replaced for the combination is to be placed
View SolutionDeduce the equivalent focal length of two convex lenses of focal lengths F1andF2 when placed in contact.
View SolutionTwo thin lenses of focal lengths f1 and f2 are in contact. The focal length of this combination is
View SolutionTwo similar thin equiconvex lenses, of focal length f each, are kept coaxially in contact with each other such that the focal length of the combination is F_1 . When the space between the two lenses is filled with glycerin (which has the same refractive index (mu = 1.5) as that of glass) then the equivalent focal length is f_2 . The ratio F_1 : F_2 will be:
View SolutionTwo thin lenses of focal lengths f1 and f2 are in contact. The focal length of this combination is
View Solution

