A current is passed through two cells connected in series. The first cell contains X(NO3)3 (aq) and the second cell contains Y(NO3)2 (aq). The relative atomic masses of X and Y are in the ratio 1:2. What is the ratio of liberated mass of X to that of Y?
3:2
1:2
1:3
3:1
The correct Answer is:D
To solve the problem, we need to find the ratio of the liberated mass of X to that of Y when a current is passed through two electrochemical cells connected in series.
1. Identify the Atomic Masses:
- Let the atomic mass of X be A.
- Given that the atomic mass of Y is in the ratio of 1:2 with X, we can express the atomic mass of Y as 2A.
2. Determine the Equivalent Weights:
- The equivalent weight is defined as the atomic mass divided by the valency.
- For X, which is in the form X(NO3)3, the valency is 3 (since it can donate 3 electrons). Thus, the equivalent weight of X is:
Equivalent weight of X=A3
- For Y, which is in the form Y(NO3)2, the valency is 2 (since it can donate 2 electrons). Thus, the equivalent weight of Y is:
Equivalent weight of Y=2A2=A
3. Establish the Relationship Between Masses:
- The mass of a substance liberated during electrolysis is directly proportional to its equivalent weight. Therefore, we can write:
Mass of XMass of Y=Equivalent weight of XEquivalent weight of Y
- Substituting the equivalent weights we calculated:
Mass of XMass of Y=A3A
4. Simplify the Ratio:
- Simplifying the right-hand side:
Mass of XMass of Y=A/3A=13
5. Conclusion:
- The ratio of the liberated mass of X to that of Y is:
Mass of X:Mass of Y=1:3
Final Answer:
The ratio of the liberated mass of X to that of Y is 1:3.
- Let the atomic mass of X be A.
- Given that the atomic mass of Y is in the ratio of 1:2 with X, we can express the atomic mass of Y as 2A.
- The equivalent weight is defined as the atomic mass divided by the valency.
- For X, which is in the form X(NO3)3, the valency is 3 (since it can donate 3 electrons). Thus, the equivalent weight of X is:
Equivalent weight of X=A3
- For Y, which is in the form Y(NO3)2, the valency is 2 (since it can donate 2 electrons). Thus, the equivalent weight of Y is:
Equivalent weight of Y=2A2=A
- The mass of a substance liberated during electrolysis is directly proportional to its equivalent weight. Therefore, we can write:
Mass of XMass of Y=Equivalent weight of XEquivalent weight of Y
- Substituting the equivalent weights we calculated:
Mass of XMass of Y=A3A
- Simplifying the right-hand side:
Mass of XMass of Y=A/3A=13
- The ratio of the liberated mass of X to that of Y is:
Mass of X:Mass of Y=1:3
The ratio of the liberated mass of X to that of Y is 1:3.
Topper's Solved these Questions
- ELECTROCHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - EFFICIENT
46 Videos
- CLASSIFICATION OF ELEMENTS AND PERIODICITY IN PROPERTIES BOOK - VMC MODULES ENGLISHCHAPTER - CLASSIFICATION OF ELEMENTS AND PERIODICITY IN PROPERTIES EXERCISE - JEE ADVANCE (ARCHIVE)
30 Videos
- ENVIRONMENTAL CHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - ENVIRONMENTAL CHEMISTRYEXERCISE - JEE Main (Archive)
39 Videos
Similar Questions
A current is passed through 2 voltmeters connected in series. The first voltmeter contians XSO4)(aq) and second has Y2SO4(aq). The relative atomic masses of X and Y are in the ratio 2:1. The ratio of the mass of X liberated to the mass of Y liberated is:
View SolutionA compound contains elements X and Y in 1 : 4 mass ratio. If the atomic masses of X and Y are in ratio 1 : 2, then empirical formula will be
View SolutionIn an electrolysis experiment, current was passed for 5h through two cells connected in series. The first cell contains a solution of gold and second contains copper sulphate solution. In the first cell, 9.85g of gold was deposited. If the oxidation number of gold is +3, find the amount of copper deposited at the cathode of the second cell. Also calculate the magnitude of the current in ampere, ( Atomic weight of Au is 1197 and atomic weight of Cu is 63.5).
View SolutionFind the equation of a line passes through (3,4) and the ratio of its intercepts on X and Y-axis is 3:2.
View SolutionAn electric current is passed through electrolytic cells in series one containing Ag(NO3)(eq) and other H2SO4 (aq). What volume of O2 measured at 25∘C and 750mm Hg pressure would be liberated form H2SO4 if
(a) one mole of Ag+ is deposited from AgNO3 solution
(b) 8×1022 ions of Ag+ are deposited from AgNO3 solution.
View SolutionSuppose two elements X and Y combine to form two compound XY2andX2Y3weighs 85g. The atomic masses of X and Y are respectively :
View SolutionIf same quantity of electricity is passed through three electrolytic cells containing FeSO4,Fe2(SO4)3, and Fe(NO3)3, then
View SolutionIf same quantity of electricity is passed through three electrolytic cells containing FeSO4,Fe2(SO4)3, and Fe(NO3)3, then
View Solution3 faraday electricity was passed through the three electrolytic cells connected in series containing Ag+Ca2+andAl+3 ions respectively. The molar ration in which the three metl ions are liberated at the electrodes is :
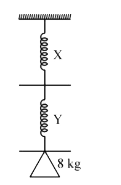
View SolutionA body of mass 8 kg is suspended through two light springs X and Y connected in series as shown in figure. The readings is X and Y respectively are :
View Solution

