Let ABCD be a quadrilateral with area 18 , side AB parallel to the side CD,andAB=2CD . Let AD be perpendicular to ABandCD . If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is a=3 (b) 2 (c) 32 (d) 1
3
2
3/2
1
The correct Answer is:B
Let CD=α. Then, AB=2α.
The equation of BC is
y=−2rα(x−2α)or,2rx+αy−4rα=0
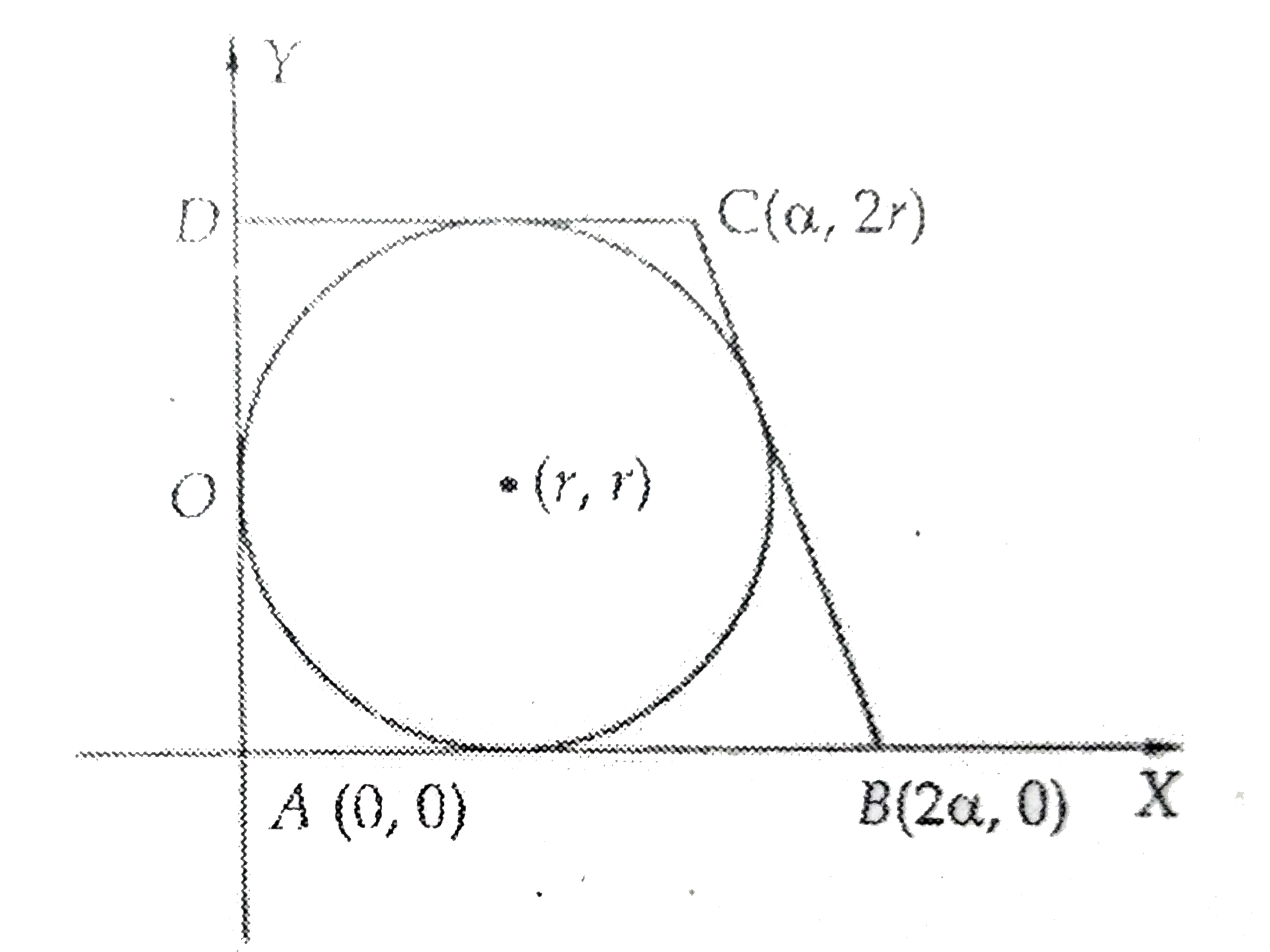
It touches the circle (x−1)2+(y−r)2=r2
∴∣∣∣2x2+αr−4αr√4r2+α2∣∣∣=r
⇒(2r2−3αr)2=r2(α2+4r2)
⇒(2r−3α)2=(α2+4r2)⇒−12rα+9α2=α2⇒α=3r2
Now, Area of quadrilateral ABCD = 18
⇒12(AB+CD)x2r=18
⇒3αr=18
⇒αr=6⇒3r2=12[∴α=3r2]
⇒r=2
Topper's Solved these Questions
- CIRCLESBook:OBJECTIVE RD SHARMA ENGLISHChapter:CIRCLESExercise:Section-I (Solved MCQs)
Explore 1 Video
- CIRCLESBook:OBJECTIVE RD SHARMA ENGLISHChapter:CIRCLESExercise:Section II - Assertion Reason Type
Explore 12 Videos
- CIRCLESBook:OBJECTIVE RD SHARMA ENGLISHChapter:CIRCLESExercise:Chapter Test
Explore 53 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:CARTESIAN PRODUCT OF SETS AND RELATIONS Exercise:Chapter Test
Explore 30 Videos
- COMPLEX NUMBERS Book:OBJECTIVE RD SHARMA ENGLISHChapter:COMPLEX NUMBERS Exercise:Chapter Test
Explore 58 Videos
Similar Questions
if one of the diameters of the circle, given by the equation, x2+y2−4x+6y−12=0, is a chord of a circles S, whose centre is at (−3,2) , then the radius of S is
View Solutionabout to only mathematics
View SolutionThe two circles x2+y2−2x+6y+6=0andx2+y2−5x+6y+15=0 touch eachother. The equation of their common tangent is : (A) x=3 (B) y=6 (C) 7x−12y−21=0 (D) 7x+12y+21=0
View SolutionIf n(A×B)=45, then n(A) cannot be
View SolutionThe locus of the center of a circle which touches the circles |z−z1|=a,|z−z2=b| externally will be
View SolutionLet A,B,C,D be the vertices of a convex quadrilateral; K,L,M,N the midpoints of the sides; X,Y,Z,T, intersection of the lines joining vertices to midpoints of opposite sides and a,b,c,d areas of portion of the figure in quadrilateral. find the area of quadrilateral XYZT in terms of a,b,c and d.
View SolutionLet ABCD be perpendicular to AB and CD. If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is : (a) 3 (b) 2 (c) 32( d ) 1
View SolutionLet ABCD be a quadrilateral with area 18 , side AB parallel to the side CD,andAB=2CD . Let AD be perpendicular to ABandCD . If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is 3 (b) 2 (c) 32 (d) 1
View SolutionABCD is a trapezium with parallel sides AB=a and DC=b. If EandF are mid-points of non-parallel sides ADandBC respectively, then the ratio of areas of quadrilaterals ABFEandEFCD is:
(a) a:b
(b) (a+3b):(3a+b)
(c) (3a+b):(a+3b)
(d) (3a+b):(3a+b)
View SolutionIf a,b,c,d are the side of a quadrilateral, then find the the minimuym value of a2+b2+c2d2
View SolutionLet ABCD be a quadrilateral with area 18 , side AB parallel to the side CD,andAB=2CD . Let AD be perpendicular to ABandCD . If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is a=3 (b) 2 (c) 32 (d) 1
View SolutionLet ABCD be a quadrilateral with area 18 , side AB parallel to the side CD,andAB=2CD . Let AD be perpendicular to ABandCD . If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is 3 (b) 2 (c) 32 (d) 1
View SolutionA circle touches all the four sides of a quadrilateral ABCD . Prove that: AB+CD=BC+DA .
View SolutionIf four sides of a quadrilateral ABCD are tangential to a circle, then AC+AD=BD+CD (b) AB+CD=BC+AD (c) AB+CD=AC+BC (d) AC+AD=BC+DB
View SolutionIn a quadrilateral ABCD , the angles A, B, C and D are in the ratio 1:2:3:4. Find the measure of each angles of the quadrilateral.
View SolutionABCD is a trapezium with parallel sides AB=a and DC=b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFE and EFCD is: a:b (b) (a+3b):(3a+b) (3a+b):(a+3b) (d) (3a+b):(3a+b)
View Solution
