Let f(x)={1−|x|,|x|≤10,|x|>1andg(x)=f(x−1)for allx∈R The value of ∫3−3g(x)dx is
2
3
4
5
The correct Answer is:A
The graph of f(x) and g(x) are shown in Fig. 14 and 15 respectively.
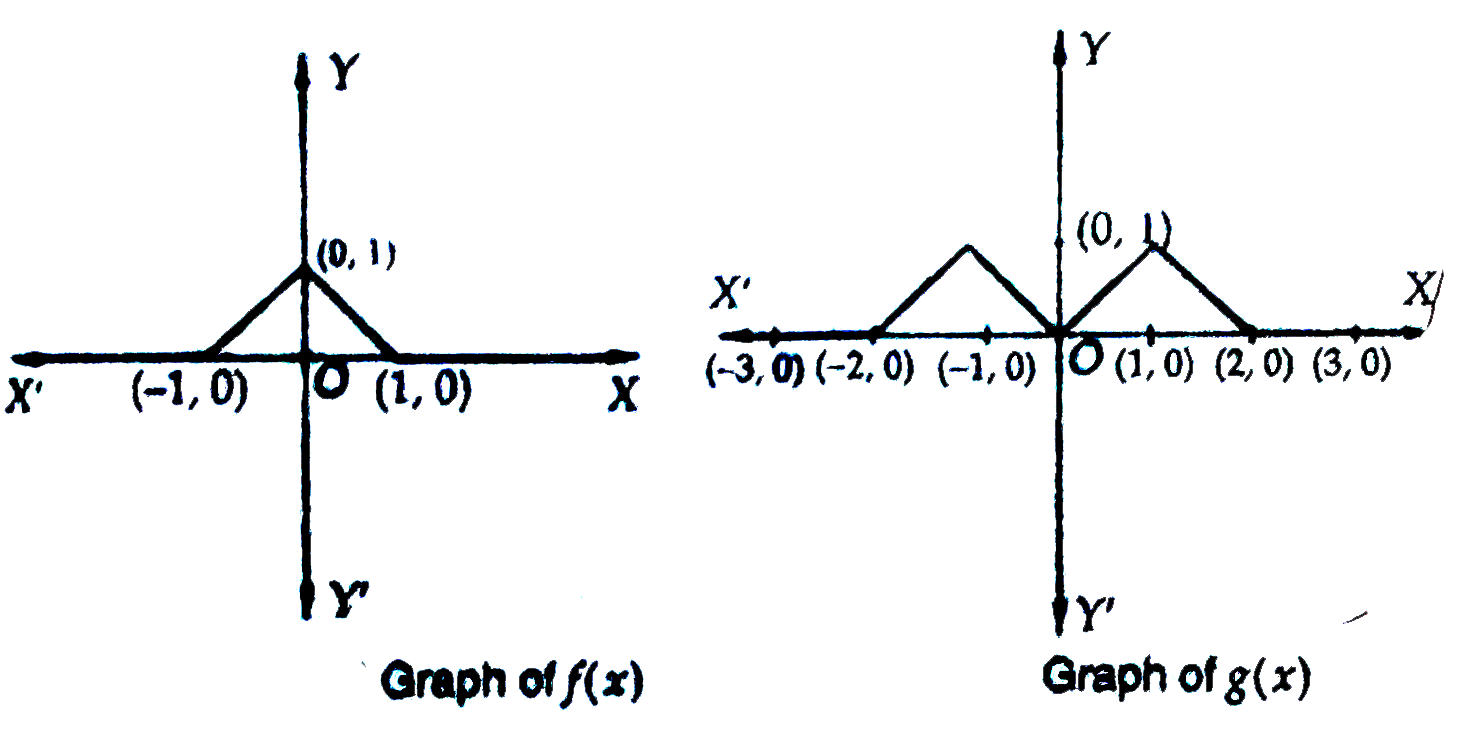
Clearly,
3∫−3g(x)dx=−2∫−30dx+0∫−2f(x)dx+2∫0f(x)dx+3∫20dx
⇒3∫−3g(x)dx=22∫0f(x)dx=2(12×2×1)=2
Topper's Solved these Questions
- DEFINITE INTEGRALSBook:OBJECTIVE RD SHARMA ENGLISHChapter:DEFINITE INTEGRALSExercise:Section II - Assertion Reason Type
Explore 12 Videos
- DEFINITE INTEGRALSBook:OBJECTIVE RD SHARMA ENGLISHChapter:DEFINITE INTEGRALSExercise:Exercise
Explore 143 Videos
- DEFINITE INTEGRALSBook:OBJECTIVE RD SHARMA ENGLISHChapter:DEFINITE INTEGRALSExercise:Chapter Test 2
Explore 56 Videos
- CONTINUITY AND DIFFERENTIABILITYBook:OBJECTIVE RD SHARMA ENGLISHChapter:CONTINUITY AND DIFFERENTIABILITYExercise:Exercise
Explore 87 Videos
- DERIVATIVE AS A RATE MEASURER Book:OBJECTIVE RD SHARMA ENGLISHChapter:DERIVATIVE AS A RATE MEASURER Exercise:Exercise
Explore 26 Videos
Similar Questions
Statement-1: ∫π/20xcotxdx=π2log2
Statement-2: ∫π/20logsinxdx=−π2log2
View SolutionIf I=∫2−2dx, then I equals
View SolutionThe value of the integral ∫20x[x]dx
View SolutionThe function f(x)=4−x24x−x3 is discontinuous at
View SolutionThe edge of a cube is equal to the radius of a sphere. If the edge and the radius increase at the same rate, then the ratio of the increases in surface areas of the cube and sphere is
View SolutionConsider f g and h are real-valued functions defined on R. Let f(x)-f(-x)=0 for all x in R, g(x) + g(-x)=0 for all x in R and h (x) + h(-x)=0 for all x in R. Also, f(1) = 0,f(4) = 2, f(3) = 6, g(1)=1, g(2)=4, g(3)=5, and h(1)=2, h(3)=5, h(6) = 3 The value of f(g(h(1)))+g(h(f(-3)))+h(f(g(-1))) is equal to
View SolutionLet f(x)={1-|x|,|x|<=1 and 0,|x|<1 and g(x)=f(x-)+f(x+1) ,for all x in R .Then,the value of int_(-3)^(3)g(x)dx is
View Solutionf(x):[0,5]→R,F(x)=∫x0x2g(x), f(1) = 3
g(x) = ∫x1f(t)dt then correct choice is
View SolutionLet f(x)={1−|x|,|x|≤10,|x|>1andg(x)=f(x−1)for allx∈R The graph for g(x) is given by
View SolutionIf f(x)=f(4−x),g(x)+g(4−x)=3 and ∫40f(x)dx=2, then : ∫40f(x)g(x)dx=
View SolutionIf f(x)+f(π−x)=1 and g(x)+g(π−x)=1, then : ∫π0[f(x)+g(x)]dx=
View SolutionIf g(x)=12[f(x)−f(−x)] defined over −3≤x≤3 and f(x)=2x2−4x+1, then the value of ∫3−3g(x)dx is -
View SolutionLetf(x)=g(x)∣∣(x−1)(x−2)(x−3)2(x−4)3∣∣, where g(x)=x3+bx2+cx+d. if f(x) is differentiable for all x∈Randf'(3)+f'''(4)=0 then the value of g(5) is ______.
View SolutionLet f:R→R is defined by f(x)={(x+1)3x≤1lnx+(b2−3b+10)x>1 If f (x) is invertible, then the set of all values of 'b' is :
View SolutionLet f(x) be a function satisfying f'(x)=f(x) with f(0)=1 and g(x) be the function satisfying f(x)+g(x)=x2.Prove that,
∫10f(x)g(x)dx=12(2e−e2−3)
View Solutionमाना g(x) = 1+x - [x]और f(x)=⎧⎪⎨⎪⎩−1x<00x=01x>0 तब x के सभी मानों के लिए f(g(x)) का मान है:
View Solution
