If f(x) =x2∫x(t−1)dt,1≤x≤2 then the greatest value of ϕ (x) , is
2
4
8
none of these
The correct Answer is:B
We have ,
f(x)=x2∫x(t−1)dt
⇒f(x)=2x(x2−1)−(x−1)
⇒f(x)=2x3−3x+1
⇒f'(x)=(x−1)(2x2+2x−1)
⇒f(x)−2(x−1)(x+√3+12)(x−√3−12)
The signs of f(x) for different values for x are shown in Fig.26
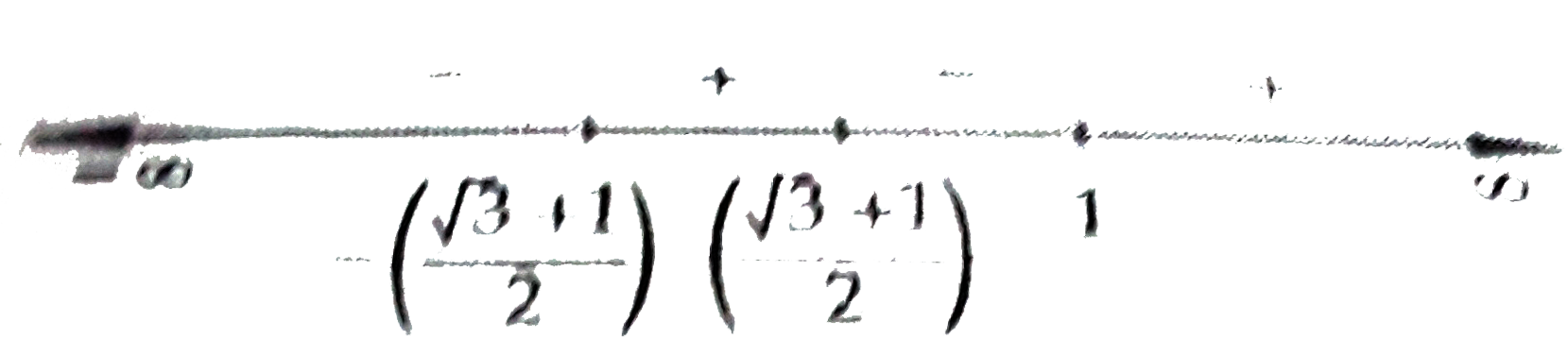
Clearly f'(x) >0 for all x∈[1,2] So, f(x) is increasing on [ 1.2]
Hence ,greatest value of f(x) is equal to
f(2)=4∫2[(t−1)22]42=4
Topper's Solved these Questions
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Section II - Assertion Reason Type
7 Videos
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Exercise
47 Videos
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Chapter Test
29 Videos
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Chapter Test
20 Videos
- MEASURES OF CENTRAL TENDENCYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test
21 Videos
Similar Questions
Statement -1 The maximum value of f(x)=13x4+8x3−18x2+60is153
Statement -2 : The function g(x) =1f(x) attains its minimum value at x=1 and x=-3
View SolutionFor the curve y=xex , the point
View SolutionThe maximum value of (1x)2x2 is
View SolutionWhich of the following sentences is a statement ?
View SolutionThe arthmetic mean of first n odd natural numbers, is
View Solutionif f(x) =[−√1−x2 , 0≤x≤1−x , x>1, then
View SolutionIf f(1x)+x2f(x)=0,x>0andI=∫x1/xf(t)dt,12≤x≤2x, then I is equal to
View Solutionf(x)=⎧⎪ ⎪⎨⎪ ⎪⎩1−x, 0≤c≤10, 1≤x≤2 and ϕ(x)=∫x0f(t) dt.Then(2−x)2, 2≤x≤3for any x∈[2,3],ϕ(x) equals
View SolutionIf f(x) =∫x2x(t−1)dt,1≤x≤2 then the greatest value of ϕ (x) , is
View SolutionLet f(x)=−x3+x2−x+1andg(x)={min(f(t)),0≤t≤xand0≤x≤1x−1,1<x≤2 Then, the value of limx→1g(g(x)), is........ .
View Solutionमूल्यांकित कीजिएः 4∫1f(x)dx, जहाँ f(x)={4x+3यदि 1≤x≤23x+5यदि 2≤x≤4
View SolutionF(x)=x2∫1cos√tdt.
Statement-1: f'(x)=cosx.
Statement-2: यदि f(x)=x∫aϕ(t)dt, तो f'(x)=ϕ(x).
View SolutionFind the range of the function f(x)=∫x0|t−1|dt, where 0≤x≤2
View Solutionयदि x∫0f(t)dt=x2+1∫xt2f(t)dt है, तो f'(12) है
View SolutionIf F(x)= int_0^(x)(cost)/((1+t^2))dt,0 le x le 2pi Then
View SolutionIf f(x)=∫x2x(t−1)dt,1≤x≤2, find the greatest value of f(x).
View Solution

