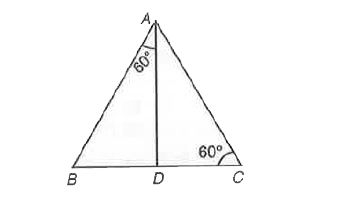
If the median AM , angle bisector AD and altitude AH drawn from vertex A of a triangle ABC divide angle A into four equal (D lying between H and M) , then
A=π3
A=π2
ACAB=√2+1
ACAB=1√2+1
To solve the problem, we need to analyze the triangle ABC with the given conditions.
1. Understanding the Problem: We have a triangle ABC where the median AM, angle bisector AD, and altitude AH from vertex A divide angle A into four equal parts. Let each of these parts be denoted as θ. Therefore, we can express angle A as:
∠A=4θ
2. Identifying Angles in Triangle AHB: Since AH is an altitude, we know that:
∠AHB=90∘
This gives us:
∠BAH=θand∠ABH=90∘−θ
3. Finding Angle C: In triangle AHC, we can express the angles as follows:
∠AHC=90∘and∠CAH=3θ
Therefore, we can write:
∠A+∠C+∠B=180∘
Substituting the known angles:
90∘+3θ+(90∘−θ)=180∘
Simplifying this gives:
180∘+2θ=180∘⟹2θ=0⟹θ=0
This is not possible since θ must be a positive angle.
4. Using the Sine Rule: We will apply the sine rule in triangles AMB and AMC:
- For triangle AMB:
AMsin(90∘−θ)=BMsin(3θ)
This simplifies to:
BM=AM⋅cos(θ)⋅sin(3θ)
- For triangle AMC:
AMsin(90∘−3θ)=CMsin(θ)
This simplifies to:
CM=AM⋅cos(3θ)⋅sin(θ)
5. Setting BM = CM: Since M is the midpoint (median), we have:
BM=CM
Therefore:
AM⋅cos(θ)⋅sin(3θ)=AM⋅cos(3θ)⋅sin(θ)
Canceling AM from both sides (assuming AM≠0):
cos(θ)⋅sin(3θ)=cos(3θ)⋅sin(θ)
6. Using Trigonometric Identities: We can use the identity for sine:
sin(3θ)=3sin(θ)−4sin3(θ)
and substitute it into the equation:
cos(θ)(3sin(θ)−4sin3(θ))=cos(3θ)sin(θ)
7. Solving for θ: After simplifying, we find:
6θ=180∘−2θ⟹8θ=180∘⟹θ=22.5∘
Thus:
∠A=4θ=90∘=π2
8. Conclusion: Therefore, the value of angle A is:
∠A=π2
The correct option is:
Option 2: A=π2
∠A=4θ
∠AHB=90∘
This gives us:
∠BAH=θand∠ABH=90∘−θ
∠AHC=90∘and∠CAH=3θ
Therefore, we can write:
∠A+∠C+∠B=180∘
Substituting the known angles:
90∘+3θ+(90∘−θ)=180∘
Simplifying this gives:
180∘+2θ=180∘⟹2θ=0⟹θ=0
This is not possible since θ must be a positive angle.
- For triangle AMB:
AMsin(90∘−θ)=BMsin(3θ)
This simplifies to:
BM=AM⋅cos(θ)⋅sin(3θ)
AMsin(90∘−3θ)=CMsin(θ)
This simplifies to:
CM=AM⋅cos(3θ)⋅sin(θ)
BM=CM
Therefore:
AM⋅cos(θ)⋅sin(3θ)=AM⋅cos(3θ)⋅sin(θ)
Canceling AM from both sides (assuming AM≠0):
cos(θ)⋅sin(3θ)=cos(3θ)⋅sin(θ)
sin(3θ)=3sin(θ)−4sin3(θ)
and substitute it into the equation:
cos(θ)(3sin(θ)−4sin3(θ))=cos(3θ)sin(θ)
6θ=180∘−2θ⟹8θ=180∘⟹θ=22.5∘
Thus:
∠A=4θ=90∘=π2
∠A=π2
The correct option is:
Option 2: A=π2
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBook:OBJECTIVE RD SHARMA ENGLISHChapter:PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMExercise:SOLVED MCQ
Explore 2 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBook:OBJECTIVE RD SHARMA ENGLISHChapter:PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMExercise:Section II - Assertion Reason Type
Explore 13 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBook:OBJECTIVE RD SHARMA ENGLISHChapter:PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMExercise:Chapter Test
Explore 55 Videos
- PLANE AND STRAIGHT LINE IN SPACE Book:OBJECTIVE RD SHARMA ENGLISHChapter:PLANE AND STRAIGHT LINE IN SPACE Exercise:Chapter Test
Explore 31 Videos
- REAL FUNCTIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:REAL FUNCTIONS Exercise:Chapter Test
Explore 58 Videos
Similar Questions
P is a point on the altitude of !ABC such that ∠CBP= B3 ,then A.P.is equal to

View SolutionStatement I: If in a triangle ABC,sin2A+sin2B+sin2C=2, then one of the angles must be 90∘.
Statement II: In any triangle ABC cos2A+cos2B+cos2C=−1−4cosAcosBcosC
View SolutionIf the sides of a triangle are in the ratio 3:7:8, then find R:r
View SolutionThe length of the perpendicular from the origin to the plane passing through the point →a and containing the line →r=→b+λ→c
View SolutionThe period of the function f(x)=sin43x+cos43x, is
View SolutionIn /_ABC with usual notation,if A=3C and acute angle between altitude from vertex A and angle bisector of vertex B is 60^(@), then
View SolutionFind the angle of a triangle in which the latitude and a median drawn from the same vertex divide the angle at that vertex into 3 equal parts.
View SolutionIn /_ABC, perpendicular BE is drawn from vertex B on internal angle bisector from vertex A such that it divide /_B in 1:2 (point E lies on internal angle bisector from vertex A and lies inside Delta ABC) and Delta ABE is isoceless,then value of /_C will be
View SolutionA perpendicular drawn from a vertex to the opposite side of a triangle is known as an altitude (b) a median (c) an angle bisector a bisector
View SolutionProve that median from the vertex of an isosceles Triangle is the bisector of the vertical angle
View Solutionसिद्ध कीजिय की एक त्रिभुज के एक आधार कोण के अन्तः संदुविभाजक और दूसरे आधार कोण के बाहः अम्दविभाजक के बिच का कोण त्रिभुज के शीर्ष कोण के आधे के बराबर होता है।
View SolutionIf the median AM , angle bisector AD and altitude AH drawn from vertex A of a triangle ABC divide angle A into four equal (D lying between H and M) , then
View Solutionकिसी त्रिभुज ABC में मध्यकायें AD और खींची जाती है| यदि AD =4 ∠DAB=π6 और ∠ABE=π3 तब ,ΔABC का क्षेत्रफल बराबर है|
View SolutionIf the median AD to the side BC of a ΔABC is also an angle bisector of ∠A then ABAC is ………..
View SolutionΔABC में AD माध्यिका है तथा ∠A=60∘तब, 4AD2 बराबर है
View Solution
