Six wires of current I1=1A,I2=2A,I3=3A,I4=1A,I5=4AandI6=5A, cut the page perpendicularly at points 1, 2, 3, 4, 5 and 6. The value of line integral of B around the dotted closed path (i.e. o∫→B.d→l) is
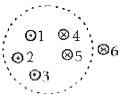
A
zero
B
μ0Wbm−1
C
2μ0Wbm−1
D
4μ0Wbm−1
Text Solution
The correct Answer is:B
(b) ∮→.d→l=μ0× Total current enclosed
μ0[I1+I2+I3+I4+I5)
=μ0[1+2+3+(−1)+(−4)]=μ0Wbm−1
|
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:MTG GUIDEChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(FORCE ON A MOVING CHARGE IN UNIFORM ELECTRIC AND MAGNETIC FIELDS)
Explore 37 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:MTG GUIDEChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(CYCLOTRON)
Explore 2 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:MTG GUIDEChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(BIOT SAVART LAW AND ITS APPLICATIONS)
Explore 47 Videos
- ELECTROSTATICSBook:MTG GUIDEChapter:ELECTROSTATICSExercise:AIPMT/NEET (MCQ.s)
Explore 28 Videos
- OPTICSBook:MTG GUIDEChapter:OPTICSExercise:AIPMT/NEET
Explore 55 Videos
Similar Questions
Knowledge Check
In figure i1=10e−2tA,i2=4A,vC=3e−2tV
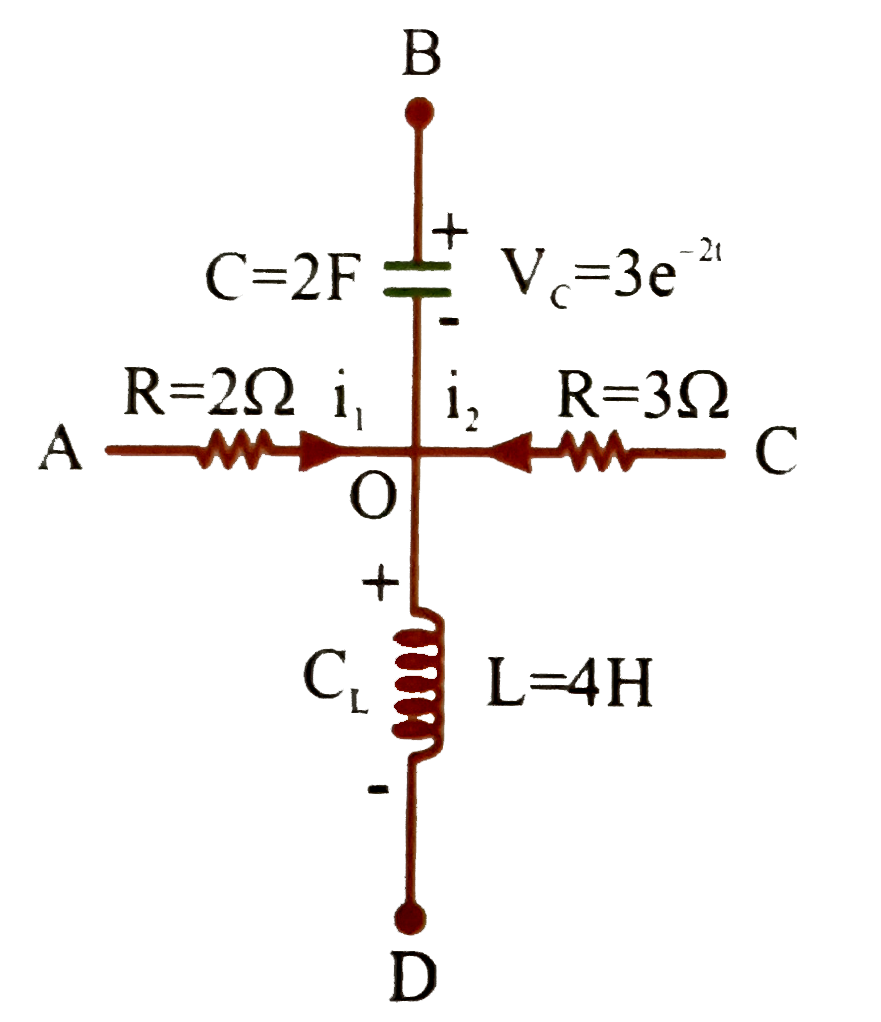
The current iL isA[2−2(1−e−2t)]AB[2+2(1−e−2t)]AC[3−2(1−e−2t)]AD[2+3(1−e−2t)]A
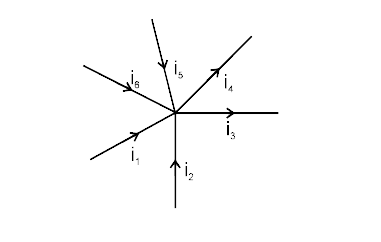
Find relation in between current i1,i2,i3,i4,i5 and i6.
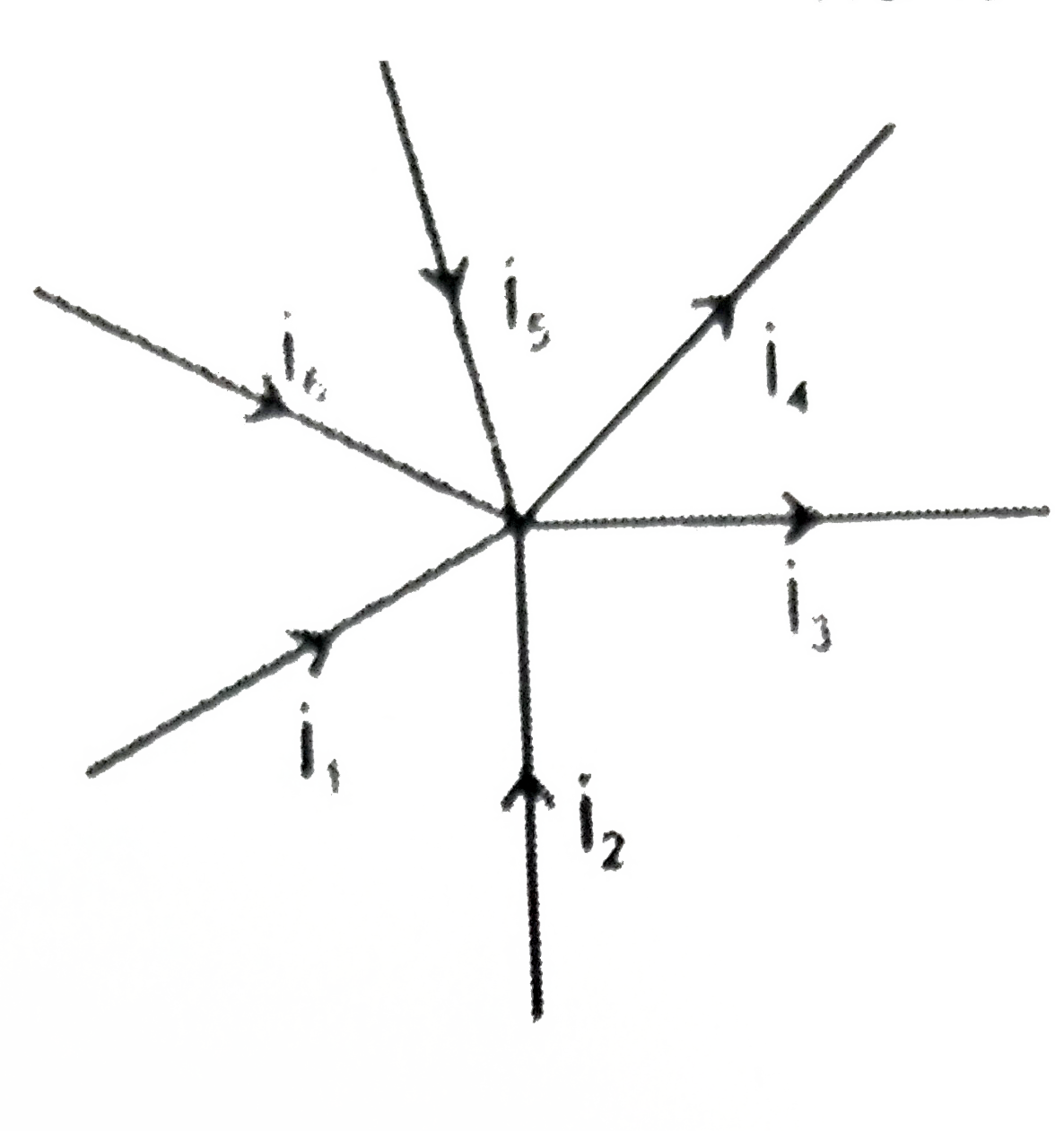
View SolutionFind relation in between current i1,i2,i3,i4,i5andi6.
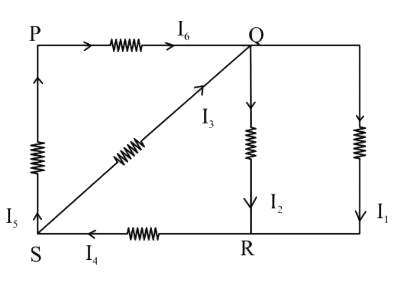
View SolutionIn the given circuit diagram, the currents, I1=−0.34,I4=0.8A, and I5=0.4A, are flowing as shown. The currents I2,I3 and I6, respectively, are :
View SolutionIf A=4i+5j and B=2i+j, calculate ,→A+→B and ∣∣→A+→B∣∣
View SolutionIf A=[1213] , then find A−1+A.
(a) I (b) 2I (c) 3I (d) 4I
View SolutionFind the argument s of z1=5+5i,z2=−4+4i,z3=−3−3iandz42−2i,
wherei=√−1.
View SolutionThe figure shows three straight current carrying conductors having current I1,I2 and I3 respectively. Calculate line integral of magnetic induction field →B along the closed path ABCDEFA

View Solution


