In Fig.
 , ar (ABQ) = ar (PBQ) and ar (BQC) = ar (BQR). Show that both the quadrilaterals ABQP and BCRQ are trapeziums.Solution in Punjabi
, ar (ABQ) = ar (PBQ) and ar (BQC) = ar (BQR). Show that both the quadrilaterals ABQP and BCRQ are trapeziums.Solution in Punjabi
Step by step video solution for In Fig. , ar (ABQ) = ar (PBQ) and ar (BQC) = ar (BQR). Show that both the quadrilaterals ABQP and BCRQ are trapeziums. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
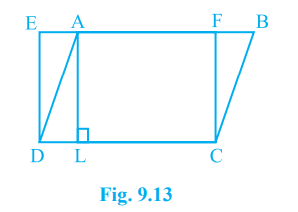
In Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that (i) ar (ABCD) = ar (EFCD) (ii) ar (ABCD) = DC × AL
View SolutionGiven an arc of a circle, complete the circle.
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn Fig, find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_032_Q01.png" width="80%"gt
View Solutionआकृति में ar(DRC)=ar(DPC) है और ar(BDP)=ar(ARC) है । दर्शाइए की दोनों चतुर्भुज ABCD और DCPR समलंब है ।
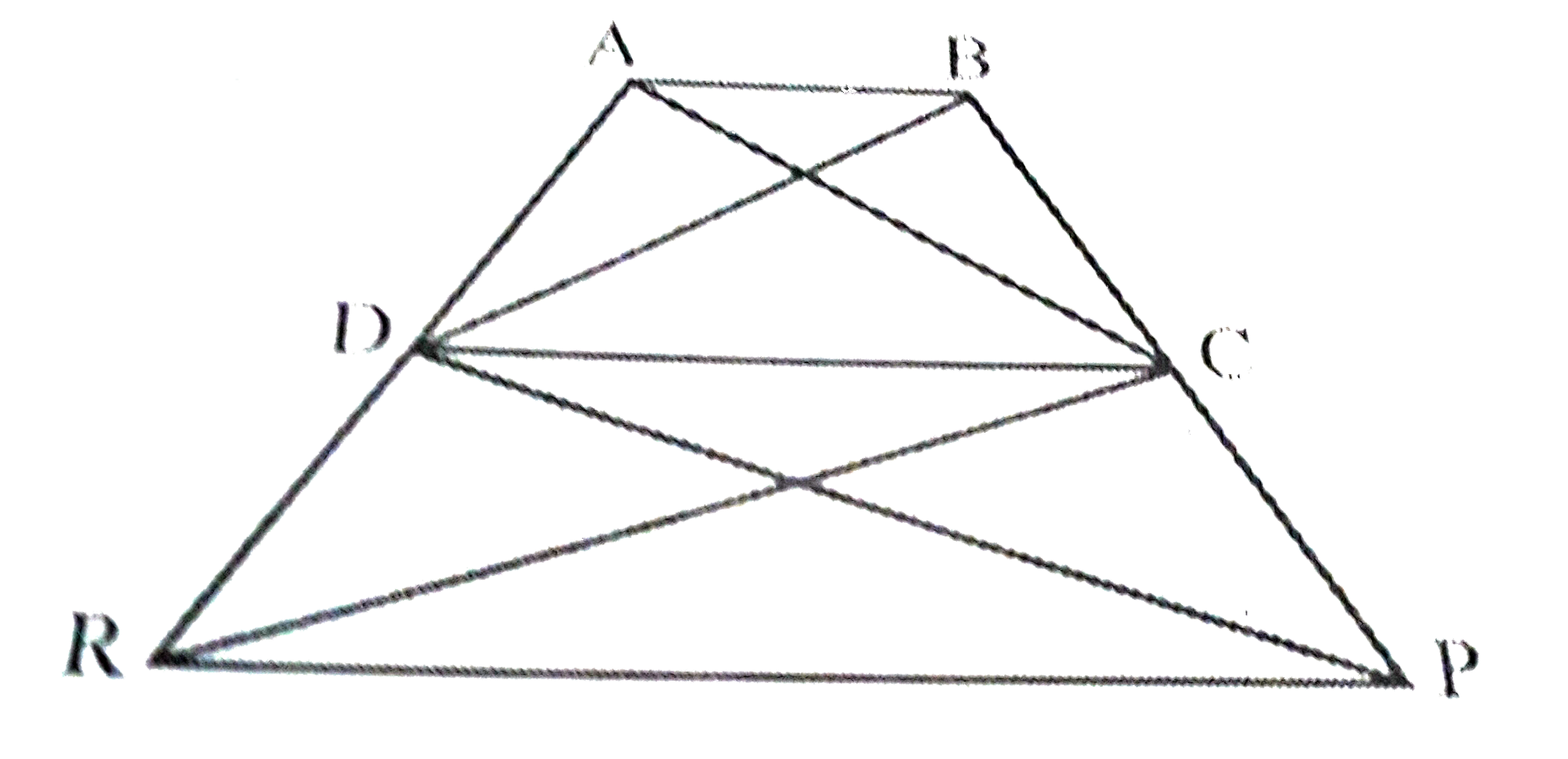
View SolutionIn the given figure , ar (DRC) = ar ( DPC) and ar(BDP) = ar(ARC) . Show that both the quadrillaterals ABCD and DCPR are trapeziums.

View SolutionIn the figure, if ar ΔRAS=arΔRBSand[ar(ΔQRB)=ar(ΔPAS) then show that both the quadrilaterals PQSR and RSBA are trapeziums.
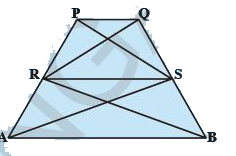
View SolutionIn the figure, if ar (DeltaRAS)_ = ar (DeltaRBS) and [ar (DeltaQRB) = ar(DeltaPAS) then show that both the quadrilaterals PQSR and RSBA are trapeziums.
View SolutionIn the figure, if ar ΔRAS=arΔRBSand[ar(ΔQRB)=ar(ΔPAS) then show that both the quadrilaterals PQSR and RSBA are trapeziums.

View Solution