P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD such that AC ⊥ BD. Prove that PQRS is a rectangle.
Given, ABCD is a rhombus and P, Q, R and S are mid-points of AB, BC, CD and DA.
∴ by mid-point theorem,
InΔADC, SR||ACandSR=12AC ...(1)
InΔABC, PQ||ACandPQ=12AC ...(2)
From (1) and (2), we get
PQ||SRandPQ=SR=12AC
∴PQRSis a parallelogram. (∵one pair of opposite sides is equal and parallel)
Now, we know that diagonals of a rhombus bisect each other at right angles.
∴ ∠EOF=90∘
Now, RQ||BD (by mid-point theorem)
⇒ RE||FO
Also, SR||AC [from (1)]
⇒ FR||OE
∴OERFis parallelogram. (∵pairs of opposite sides are parallel)
So, ∠ERF=∠EOF=90∘
(∵pairs of opposite sides are parallel)
Thus, PQRS is a parallelogram with ∠R=90∘.
Hence, PQRS is a rectangle.

Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Exercise 8b
Explore 15 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Revision Exercise (long Answer Questions)
Explore 5 Videos
- PROBABILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICSExercise:Revision Exercise
Explore 12 Videos
Similar Questions
The angles of a quadrilateral are 89∘and113∘ If the other two angles are equal, find the equal angles.
View SolutionThe sides AB and AC are equal of an isosceles triangle ABC. D E and F are the mid-points of sides BC, CA and AB respectively. Prove that:
(i) Line segment AD is perpedicular to line segment EF.
(ii) Line segment AD bisects the line segment EF.
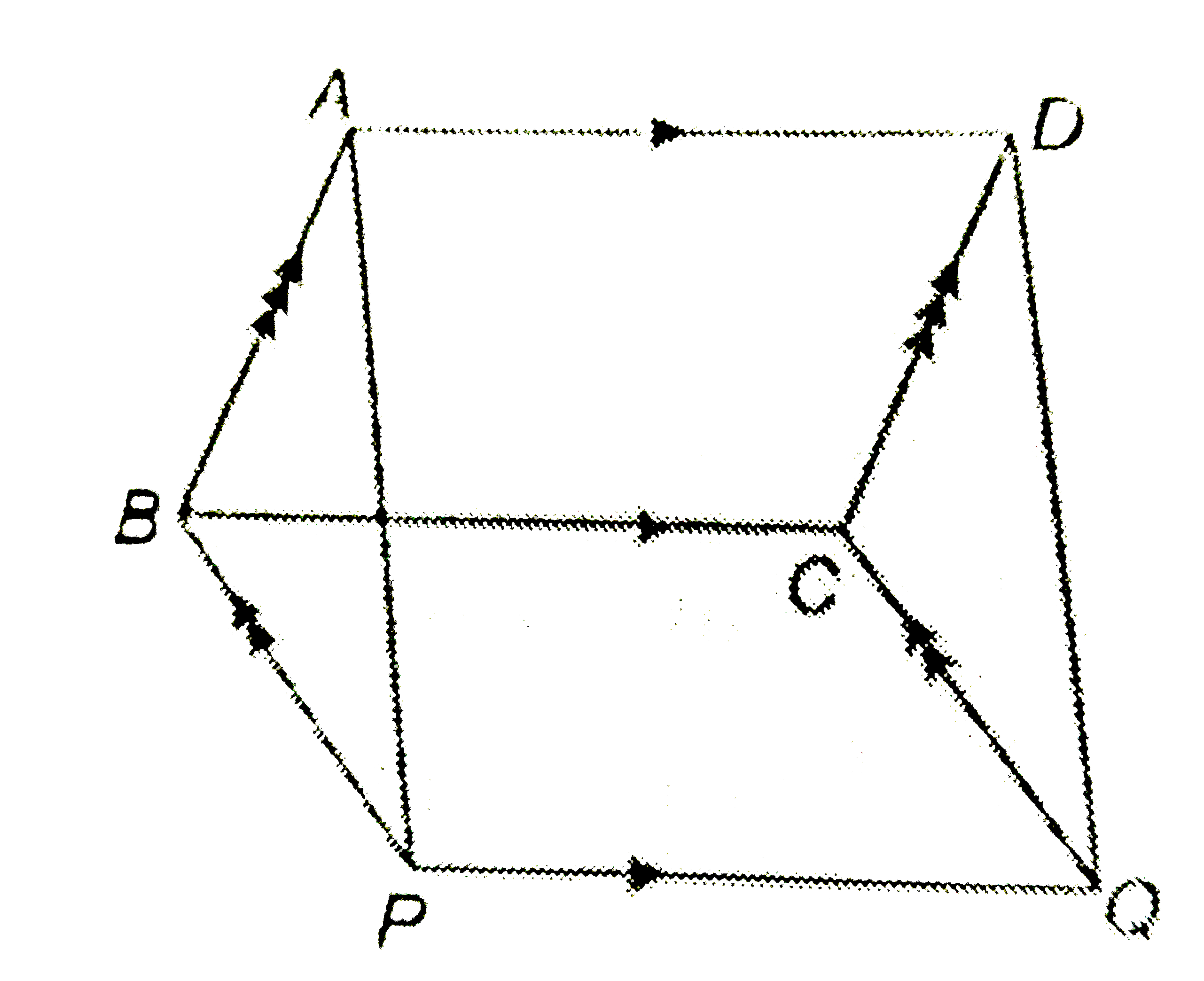
View SolutionIn the adjoining figure, ABCD and PBCQ are paralelograms. Prove that
ΔABP≅ΔDCQ
View SolutionWhat is the probability of an impossible event?
View SolutionIf the heights of 5 persons are 140 cm, 150 cm, 152 cm, 158 cm and 161 cm respectively, find the mean height.
View SolutionABCD is a rhombus and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionP, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and AC⊥BD. Prove that PQRS is a square.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
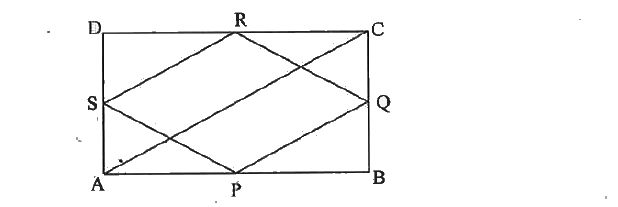
View SolutionABCD is a rectangle and P,Q,R and S are the mid points of the sides AB,BC,CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rectangle and P,R and S are the mid - points of the AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View Solution