In figure, CD∣∣AE and CY∣∣BA. Prove that ar(ΔCBX)=ar(ΔAXY).

Given : CD||AEandCY||BA
To prove: ar(ΔCBX)=ar(ΔAXY0
Proof: Since, triangle on the same base AB and between the same parallels AB and YC are equal in area, so we have
ar(ΔABC)=ar(ΔABY)
⇒ar(ΔCBX)+ar(ΔABX)=ar(ΔABX)+ar(ΔAXY)
Hence, ar(ΔCBX)=ar(ΔAXY) [cancelling ar(ΔABX) from both sides]
Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Exercise
Explore 34 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Revision Exercise (very Short Answer Questions)
Explore 10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Revision Exercise (long Answer Question)
Explore 5 Videos
- CIRCLE Book:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLE Exercise:Revision Exercise (long Answer Questions )
Explore 5 Videos
Similar Questions
The base of a parallelogram is 3 times of its corresponding height. If the area of the parallelogram is 48cm2, then find the base and the corresponding height of the parallelogram.
View SolutionThe lengths of the diagonals of a rhombus are 12 cm and 16 cm. Find the area of rhombus
View SolutionIn Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).

View SolutionAB and CD are two chords of a circle such that AB=6 cm, CD=12 cm If the distance between ABandCD is 3cm find the radius of the circle.
View SolutionIn figure, CD∣∣AE and CY∣∣BA. Prove that ar(ΔCBX)=ar(ΔAXY).

View SolutionHow many lines of symmetry does the above figure have ?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of figure given below.
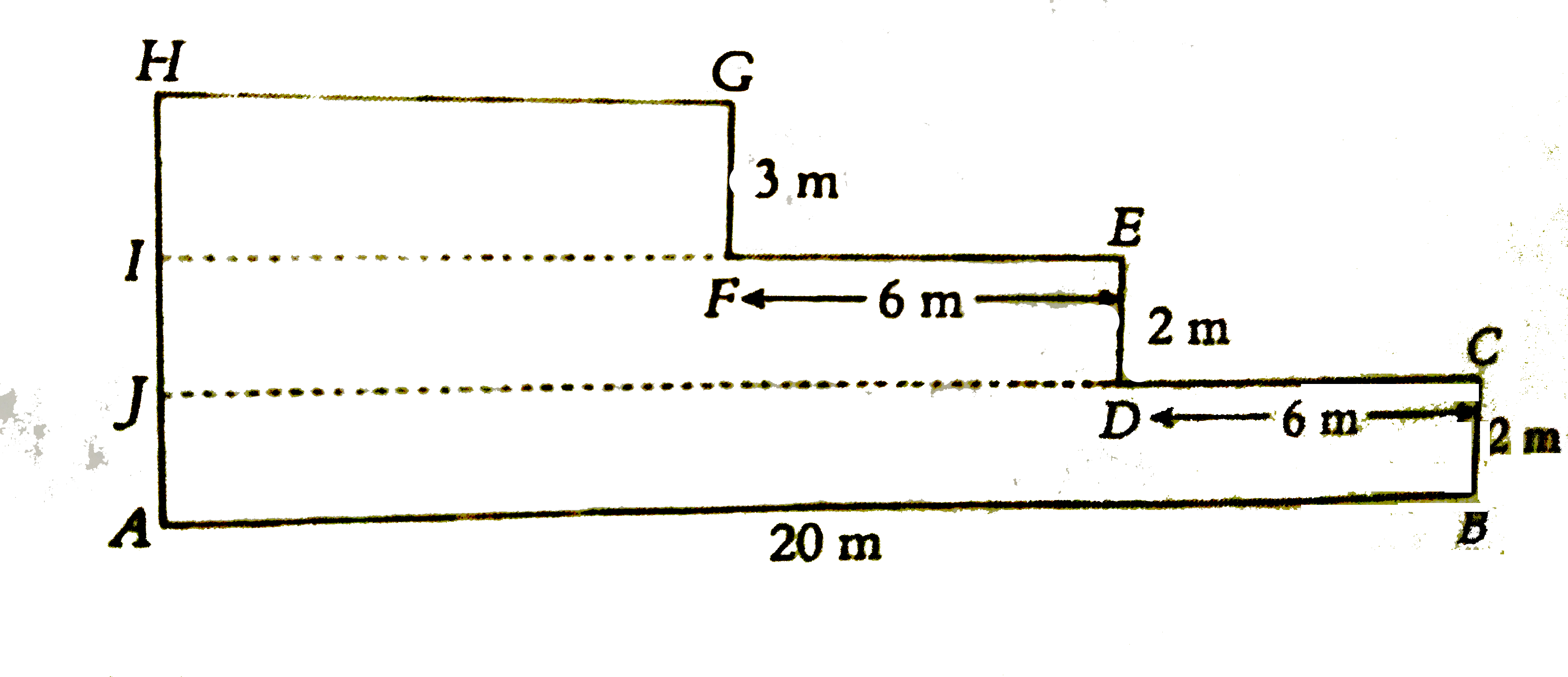
View SolutionFind the perimeter of the figure given below.
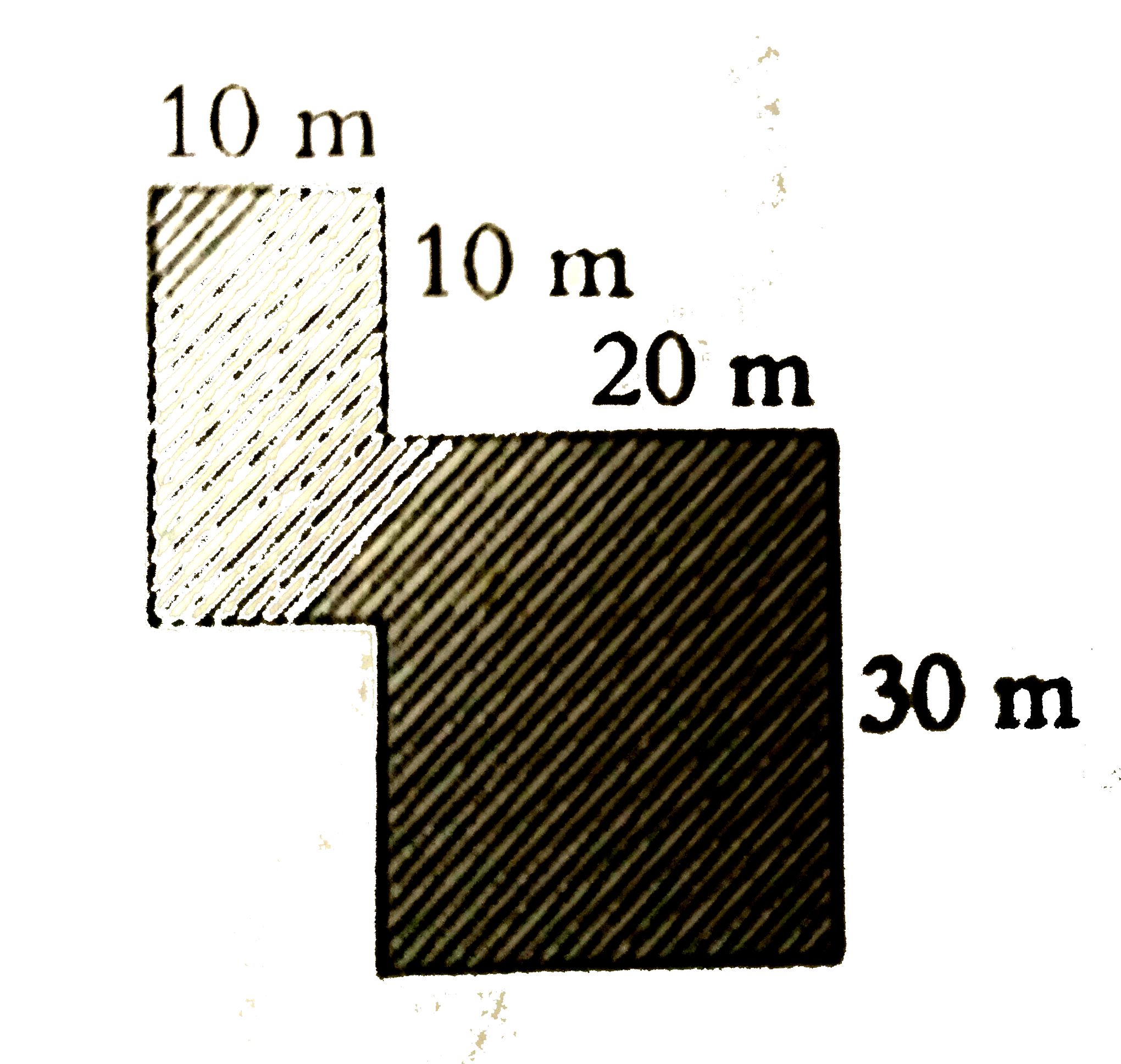
View SolutionFind the area of the figure given below.

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solution