Find out the expression for the potential energy of a system of three charges q1,q2andq3 located respectively, at r1,r2andr3 with respect to the common origin O.
Let three point charges q1,q2andq3 have position vectors r1,r2andr3.
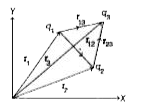
Potential energy of the charges q1andq2
U12=14πε0.q1q2|r12|
=14πε0.q1q2|r3−r1|
Similarly, U23=14πε0.q2q3|r3−r2|
⇒U13=14πε0.q1q3|r3−r1|
∴ Net potential energy of the system,
U=U12+U23+U10
U=14πε0[q1q2|r2−r2|+q2q3|r3−r2|+q1q3|r3−r1|]
সম্পর্কিত প্রশ্ন
Two unifromly charge conducting spheres of radii R1 and R2 having charges Q1 and Q2 respectively are seperated by distance r. Find total electrostatic energy of this system ?
View SolutionTwo concentric shells of radii R_(1) and R_(2) are charged uniformly with charges Q_(1) and Q_(2) respectively . Find the total electrostatic energy of the system .
View SolutionThree concentric sphereical shells of radii r1,r2 and r3 have charge q1,q2andq3 respectively . If the central sphere is now connected to the earth by a conducting wire , find the final potentials fo the three shells .
View SolutionA charge Q located at a point vec r is in equilibrium under the combined field of three charges q_(1), q_(2) and q_(3) . If the charges q_(1) and q_(2) are located at point vec r_(1) and vec r_(2) respectively, find the direction of the force on Q due to q_(3) in terms of q_(1),(q_2), vec r_(1) vec r_(2) , and vec(r) .
View SolutionTwo non-conduction hollow uniformly charged spheres of radil R_(1) and R_(2) with charge Q_(1) and Q_(2) respectively are places at a distance r. Find out total energy of the system.
View SolutionTwo concentric spherical shells of radius R1 and R2(R2>R1) are having uniformly distributed charges Q1 and Q2 respectively. Find out total energy of the system.

View SolutionTwo isolated charged metallic spheres of radii R_(1) and R_(2) having charges Q_(1) and Q_(2) respectively are connected to each other, then there is-
View Solution

