An infinte wire place along z-axis has current I1 in positive z-direction A conducting rod placed in xy plane parallel to y-axis has current I2 in positive y-direction The ends of the rod subtend +30∘ and −60∘ at the origin with positive x direction The rod is at a distance a from the origin. Find net force on the rod .
F=μ04πl1l2ln3(−ˆk)
F=μ04π2l1l(2)ln3(−ˆi)
F=μ04π2l1l2ln3(ˆk)
F=μ04π2l1l2ln3(ˆk)
The correct Answer is:A
To solve the problem of finding the net force on the conducting rod due to the infinite wire, we will follow these steps:
Step 1: Understand the Geometry
The infinite wire is placed along the z-axis and carries a current I1 in the positive z-direction. The conducting rod is in the xy-plane, parallel to the y-axis, carrying a current I2 in the positive y-direction. The ends of the rod subtend angles of +30∘ and −60∘ at the origin with respect to the positive x-direction.
Step 2: Determine the Length of the Rod
Let the distance from the origin to the rod be a. The rod extends from the angle −60∘ to +30∘. The length of the rod can be determined using the angles:
- The coordinates of the endpoints of the rod can be found using trigonometry:
- For the endpoint at +30∘:
L1=acos(30∘)=a√32
- For the endpoint at −60∘:
L2=acos(−60∘)=a12
- The length of the rod L is the difference between these two lengths:
L=L1−L2=a√32−a12=a(√32−12)
Step 3: Calculate the Force on the Rod
The force on a current-carrying conductor in a magnetic field is given by:
F=I2LB
Where B is the magnetic field due to the infinite wire. The magnetic field at a distance r from a long straight wire carrying current I1 is given by:
B=μ0I12πr
In our case, r=a.
Step 4: Substitute and Integrate
The force on the rod can be expressed as:
F=I2L(μ0I12πa)
Now, substituting the expression for L:
F=I2(a(√32−12))(μ0I12πa)
The a cancels out:
F=I2(√32−12)(μ0I12π)
Step 5: Final Expression
Now, simplifying the expression:
F=μ0I1I22π(√32−12)
Calculating √32−12=√3−12:
F=μ0I1I22π⋅√3−12
Step 6: Conclusion
Thus, the net force on the rod is:
F=μ0I1I2(√3−1)4π
The infinite wire is placed along the z-axis and carries a current I1 in the positive z-direction. The conducting rod is in the xy-plane, parallel to the y-axis, carrying a current I2 in the positive y-direction. The ends of the rod subtend angles of +30∘ and −60∘ at the origin with respect to the positive x-direction.
Let the distance from the origin to the rod be a. The rod extends from the angle −60∘ to +30∘. The length of the rod can be determined using the angles:
- The coordinates of the endpoints of the rod can be found using trigonometry:
- For the endpoint at +30∘:
L1=acos(30∘)=a√32
- For the endpoint at −60∘:
L2=acos(−60∘)=a12
- The length of the rod L is the difference between these two lengths:
L=L1−L2=a√32−a12=a(√32−12)
The force on a current-carrying conductor in a magnetic field is given by:
F=I2LB
Where B is the magnetic field due to the infinite wire. The magnetic field at a distance r from a long straight wire carrying current I1 is given by:
B=μ0I12πr
In our case, r=a.
The force on the rod can be expressed as:
F=I2L(μ0I12πa)
Now, substituting the expression for L:
F=I2(a(√32−12))(μ0I12πa)
The a cancels out:
F=I2(√32−12)(μ0I12π)
Now, simplifying the expression:
F=μ0I1I22π(√32−12)
Calculating √32−12=√3−12:
F=μ0I1I22π⋅√3−12
Thus, the net force on the rod is:
F=μ0I1I2(√3−1)4π
Similar Questions
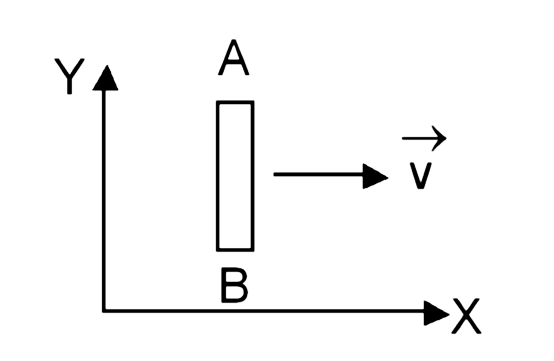
A conductor rod AB moves parallel to X-axis in a uniform magnetic field, pointing in the positive Z-direction. The end A of the rod gets-
View SolutionFind the equation of the circle whose centre lies on the positive direction of y-axis at as distance 6 from the origin and whose radius is 4.
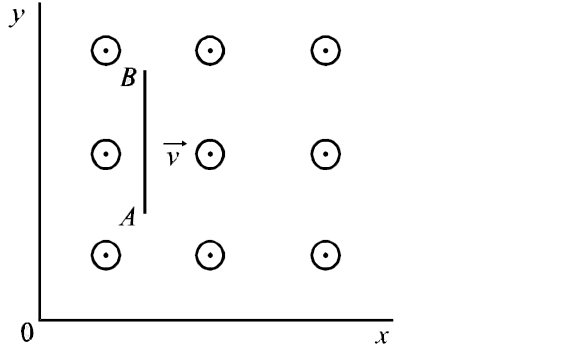
View SolutionA conducting rod AB moves parallel to the x-axis (see Fig.) in a uniform magnetic field pointing in the positive z-direction. The end A of the rod gets positively charged.
 .
.
View SolutionIf a line makes an angle of π4 with the positive directions of each of x-axis and y-axis, then the angle that the line makes with the positive direction of z-axis is
View SolutionA line makes 30∘,120∘ and 90∘ angles from the positive direction of x-axis, y-axis and π-axis respectively. Find its direction cosines.
View SolutionA single force acts on a particle situated on the negative x-axis. The torque about the origin is in the positive z-direction. The force is
View SolutionFind the equation of the line which intercepts a length 2 on the positive direction of the x-axis and is inclined at an angle of 135∘ with the positive direction of y-axis .
View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View Solution
