A uniform solid sphere of mass m, radius R moving with velocity v0 is rolling without slipping on a frictionless surface vertical wall. Ratio of magnitude of angular momentum of the sphere and after the collision about its bottommost point is
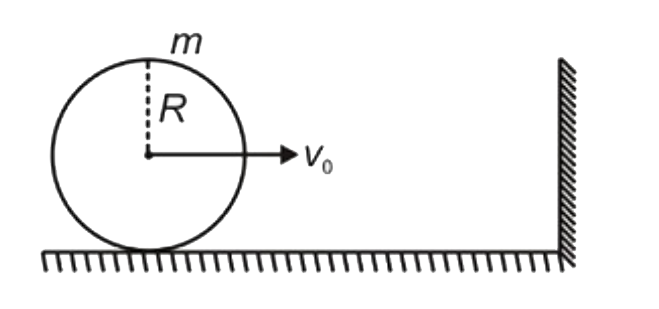
35
53
37
73
The correct Answer is:D
Step by step video solution for A uniform solid sphere of mass m, radius R moving with velocity v_0 is rolling without slipping on a frictionless surface vertical wall. Ratio of magnitude of angular momentum of the sphere and after the collision about its bottommost point is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions

A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionIf a sphere of mass m moving with velocity u collides with another identical sphere at rest on a frictionless surface, then which of the following is correct ?
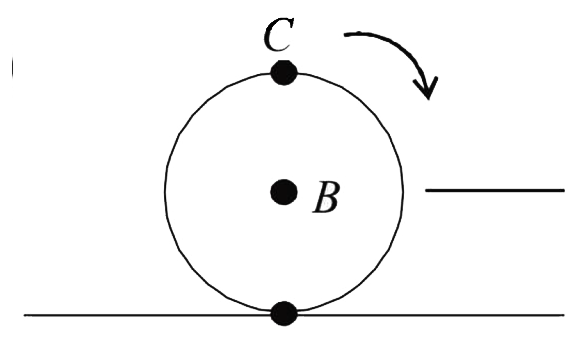
View SolutionA sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then
View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is
View SolutionA solid sphere of mass m= 500gm is rolling without slipping on a horizontal surface. Find kinetic energy of a sphere if velocity of centre of mass is 5 cm/sec
View SolutionA uniform solid sphere of mass m and radius R is suspended in vertical plane from a point on its periphery. The time period of its oscillation is
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If its radius is R, then the angular momentum of the sphere about the point of contact is.
View SolutionA uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.

View SolutionA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View SolutionA uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.

View Solution

