A stationary pulley carries a rope whose one end supports a ladder with a man and the other end the counterweight of mass M. The man of mass m climbs up a distance l with respect to the ladder and then stops. Neglecting the mass of the rope and the friction in the pulley axle, find the displacement I of the centre of inertia of this system.
mlM+m
ml2M
mlM+2m
ml2M+m
The correct Answer is:B
To solve the problem, we need to analyze the system involving a man climbing a ladder attached to a pulley with a counterweight. We will find the displacement of the center of inertia of the system step by step.
Step 1: Understand the System
We have a pulley system with:
- A counterweight of mass M on one side.
- A ladder with a man of mass m on the other side.
When the man climbs the ladder a distance l, we need to analyze the movement of the entire system.
Step 2: Identify the Forces
The forces acting on the system are:
- The weight of the counterweight M acting downwards.
- The combined weight of the man and the ladder (m+mass of ladder) acting downwards on the other side.
Since the pulley is stationary and we neglect the mass of the rope and friction, the net force along the string is zero.
Step 3: Analyze the Movement
When the man climbs a distance l relative to the ladder, the ladder and the counterweight will also move. We denote:
- The displacement of the ladder and counterweight as x0 (upward for the counterweight and downward for the ladder).
Step 4: Set Up the Equation
The displacement of the man with respect to the ground can be expressed as:
Displacement of the man=Displacement of the ladder+Displacement of the man with respect to the ladder
This can be written as:
Displacement of the man=−x0+l
Step 5: Apply Conservation of Momentum
Since there is no net force acting on the system, the total displacement of the center of mass must remain constant. Therefore, we can set up the equation for the center of mass:
m⋅(Displacement of the man)+m⋅(Displacement of the ladder)+M⋅(Displacement of the counterweight)=0
Substituting the displacements gives:
m⋅(−x0+l)+m⋅(−x0)+M⋅x0=0
Step 6: Solve for x0
Rearranging the equation:
m(−x0+l)−mx0+Mx0=0
This simplifies to:
ml−2mx0+Mx0=0
Combining terms:
ml=(2m−M)x0
Thus, we find:
x0=ml2m−M
Step 7: Find the Displacement of the Center of Inertia
The displacement of the center of inertia I can be calculated as:
I=m⋅(l−x0)+m⋅(−x0)+M⋅x02m
Substituting x0 into the equation gives us the final displacement of the center of inertia.
Final Answer
After simplifying, we find that the displacement of the center of inertia of the system is:
I=ml2m
We have a pulley system with:
- A counterweight of mass M on one side.
- A ladder with a man of mass m on the other side.
The forces acting on the system are:
- The weight of the counterweight M acting downwards.
- The combined weight of the man and the ladder (m+mass of ladder) acting downwards on the other side.
When the man climbs a distance l relative to the ladder, the ladder and the counterweight will also move. We denote:
- The displacement of the ladder and counterweight as x0 (upward for the counterweight and downward for the ladder).
The displacement of the man with respect to the ground can be expressed as:
Displacement of the man=Displacement of the ladder+Displacement of the man with respect to the ladder
This can be written as:
Displacement of the man=−x0+l
Since there is no net force acting on the system, the total displacement of the center of mass must remain constant. Therefore, we can set up the equation for the center of mass:
m⋅(Displacement of the man)+m⋅(Displacement of the ladder)+M⋅(Displacement of the counterweight)=0
Substituting the displacements gives:
m⋅(−x0+l)+m⋅(−x0)+M⋅x0=0
Rearranging the equation:
m(−x0+l)−mx0+Mx0=0
This simplifies to:
ml−2mx0+Mx0=0
Combining terms:
ml=(2m−M)x0
Thus, we find:
x0=ml2m−M
The displacement of the center of inertia I can be calculated as:
I=m⋅(l−x0)+m⋅(−x0)+M⋅x02m
Substituting x0 into the equation gives us the final displacement of the center of inertia.
After simplifying, we find that the displacement of the center of inertia of the system is:
I=ml2m
সম্পর্কিত প্রশ্ন
A rope thrown over a pulley has a on one of its ends and a counterbalancing mass M on its other end. The man whose mass is m, climbs upwards by →△r relative to the ladder and then stops. Ignoring masses of the pulley and the rope, as well as the friction the pulley axis, find the displacement of the centre of mass of this system.
View SolutionA rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
View SolutionTwo ladders are hanging from ands of a light rope passing over a light and smooth pulley. A monkey of mass 2m hangs near the bottom of one ladder whose mass is M-2m. Another monkey of mass m hangs near the bottom of the other ladder whose mass is M-m. The monkey of mass 2m moves up a distance l with respect to the ladder. The monkey of mass m moves up a distance l/2 with respect to the ladder. The displacement of centre of mass of the system is kml4M. Find the value of k.

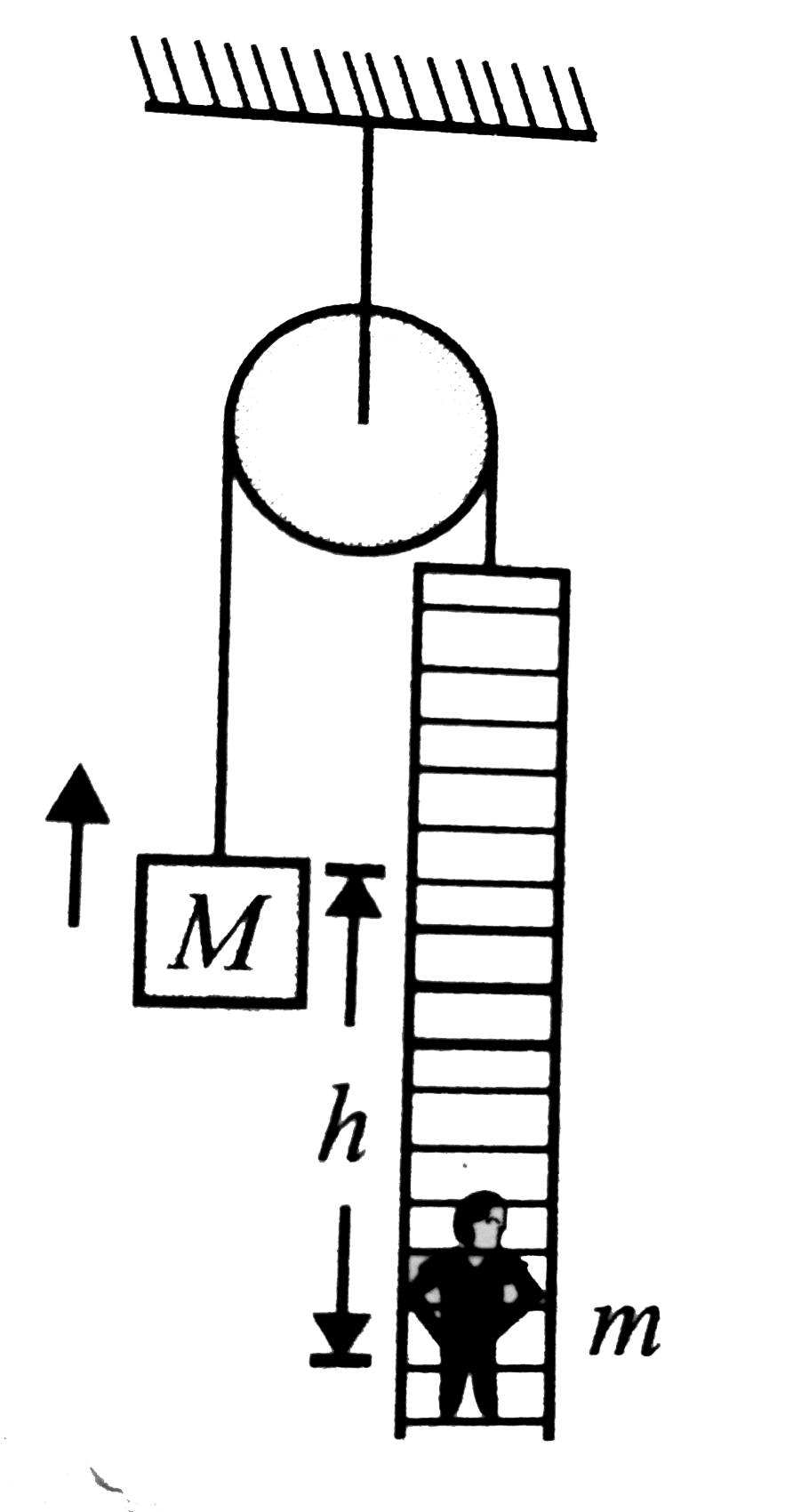
View SolutionA stationary light, smooth pulley can rotate without friction about a fixed horizontal axis. A light rope passes over the pulley. One end of the rope supports a ladder with man and the other end supports a counterweight of mass M. Mass of the man is m. initially, the centre of mass of the counterweight is at a height h from that of man as shown in Fig.
If the man starts to climb up the ladder slowly, calculate work done by him to reach his centre of mass in level with that of the counterweight.
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon

View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon

View SolutionA pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
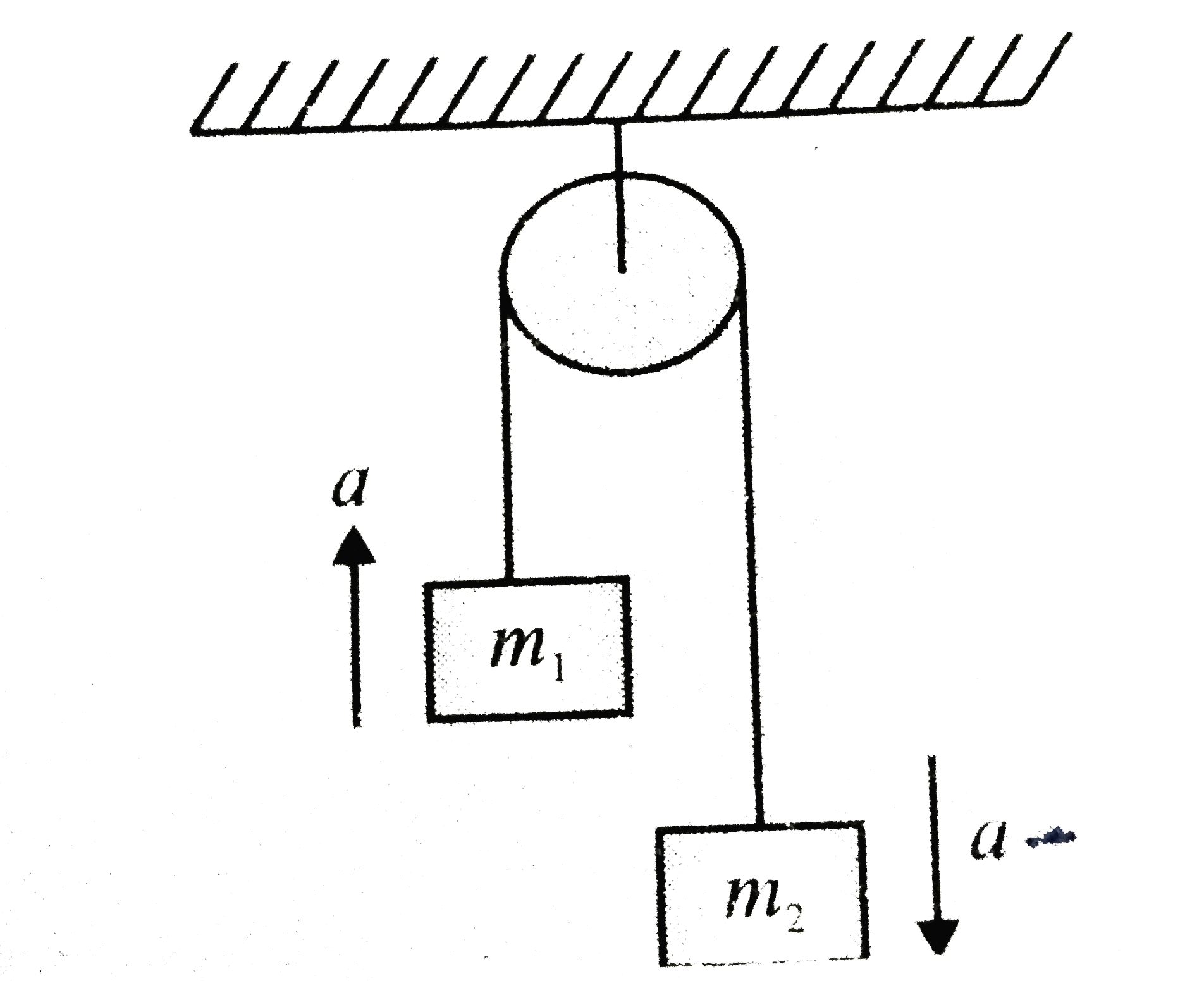
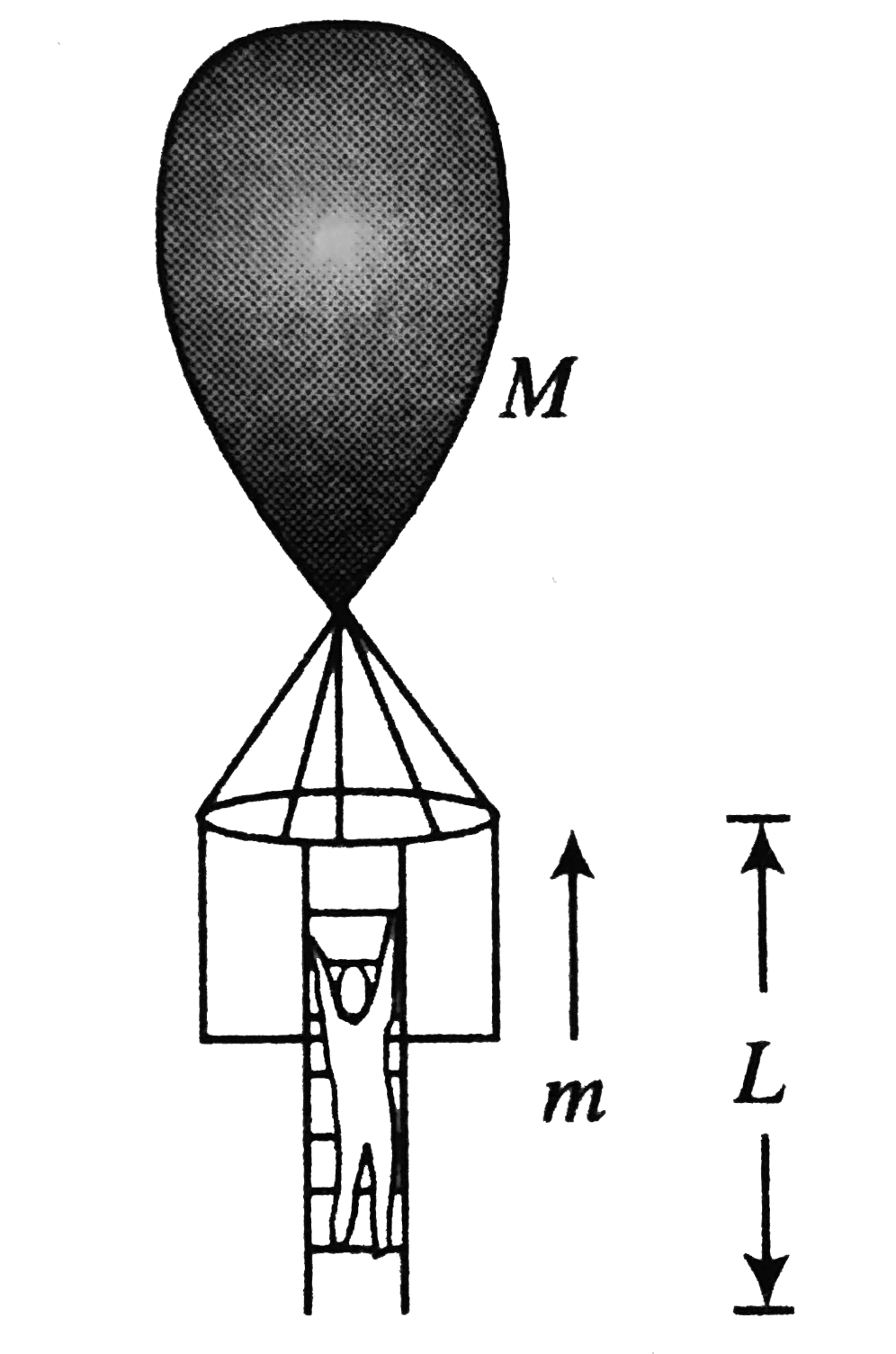
View SolutionA rope ladder of length L is attached to a balloon of mass M. As the man of mass m climbs the ladder into the balloon basket, the balloon comes down by a vertical distance s. Then the increase in potential energy of man divided by the increase in potential energy of balloon is
View SolutionA man of mass m is standing at one end of of a plank of mass M. The length of the plank is L and it rests on a frictionless horizontal ground. The man walks to the other end of the plank. Find displacement of the plank and man relative to the ground.

View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View Solution
