A charge particle q1, is at position (2, -1, 3). The electrostatic force on another charged particle q2 at (0, 0, 0) is :
q1q256πε0(2ˆi−ˆj+3ˆk)
q1q256√14ε0(2ˆi−ˆj−3ˆk)
q1q256πε0(ˆi−ˆj−3ˆk)
q1q256√14πε0(−2ˆi+ˆj−3ˆk)
The correct Answer is:D
To find the electrostatic force on a charged particle q2 at the origin (0, 0, 0) due to another charged particle q1 located at (2, -1, 3), we can follow these steps:
Step 1: Determine the Position Vectors
The position of q1 is given as →r1=(2,−1,3) and the position of q2 is →r2=(0,0,0).
Step 2: Calculate the Displacement Vector
The displacement vector →r from q1 to q2 is calculated as:
→r=→r2−→r1=(0−2)^i+(0−(−1))^j+(0−3)^k
→r=−2^i+1^j−3^k
Step 3: Calculate the Magnitude of the Displacement Vector
The magnitude r of the displacement vector →r is given by:
r=|→r|=√(−2)2+(1)2+(−3)2=√4+1+9=√14
Step 4: Determine the Unit Vector
The unit vector ^r in the direction of →r is:
^r=→r|→r|=−2^i+1^j−3^k√14
Step 5: Apply Coulomb's Law
According to Coulomb's law, the electrostatic force →F between two point charges is given by:
→F=kq1q2r2^r
where k=14πϵ0.
Step 6: Substitute Values
Substituting the values:
→F=kq1q2(√14)2^r=kq1q214^r
Substituting ^r:
→F=kq1q214(−2^i+1^j−3^k√14)
→F=kq1q214√14(−2^i+1^j−3^k)
Step 7: Final Expression
Thus, the electrostatic force on q2 due to q1 is:
→F=kq1q214√14(−2^i+1^j−3^k)
The position of q1 is given as →r1=(2,−1,3) and the position of q2 is →r2=(0,0,0).
The displacement vector →r from q1 to q2 is calculated as:
→r=→r2−→r1=(0−2)^i+(0−(−1))^j+(0−3)^k
→r=−2^i+1^j−3^k
The magnitude r of the displacement vector →r is given by:
r=|→r|=√(−2)2+(1)2+(−3)2=√4+1+9=√14
The unit vector ^r in the direction of →r is:
^r=→r|→r|=−2^i+1^j−3^k√14
According to Coulomb's law, the electrostatic force →F between two point charges is given by:
→F=kq1q2r2^r
where k=14πϵ0.
Substituting the values:
→F=kq1q2(√14)2^r=kq1q214^r
Substituting ^r:
→F=kq1q214(−2^i+1^j−3^k√14)
→F=kq1q214√14(−2^i+1^j−3^k)
Thus, the electrostatic force on q2 due to q1 is:
→F=kq1q214√14(−2^i+1^j−3^k)
Similar Questions
Three charged particle sare in equilibrium under their electrostatic forces only. Then
View SolutionIn the above question, the ratio of masses of the charge particles q1,q2,andq3 is
View SolutionSix charge of magnitude +q and −q are fixed at the corners of a regular hexagon of edge length a as shown in the figure .The electrostatic interaction energy of the charged particle is :
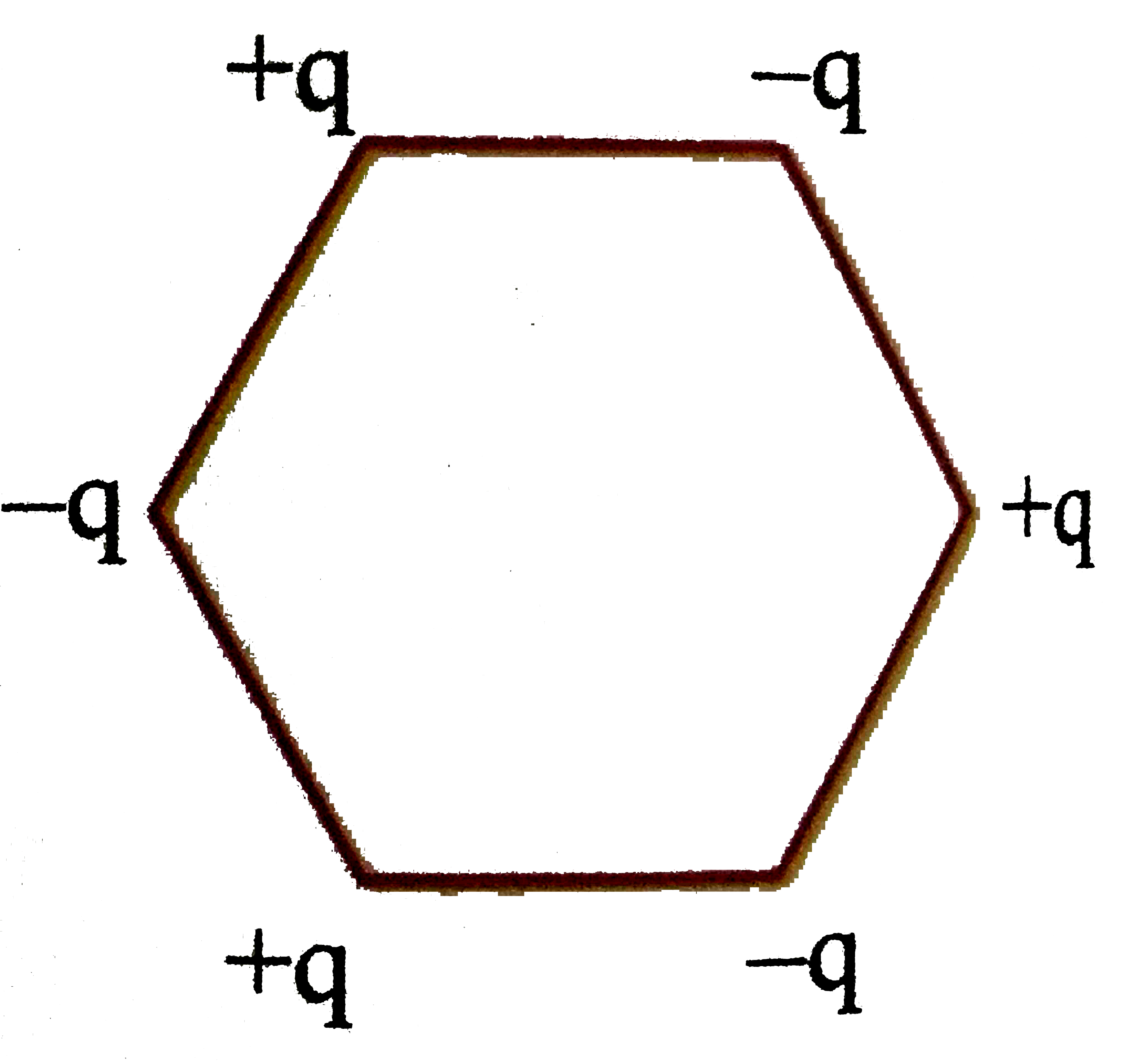
View SolutionInside a neutral hollow conducting sphere of radius X and centre C, a point charge q is placed as shown in the figure. Another point charge q1, is placed outside the sphere at distance d from centre. The net- electrostatic force on charge q placed at the centre is K=14πε0

View SolutionThree charged particles are arranged in a line,as shown in figure.Calculate the net electrostatic force on particle3 ( the -4.0μC on the right ) due to the other two charges.
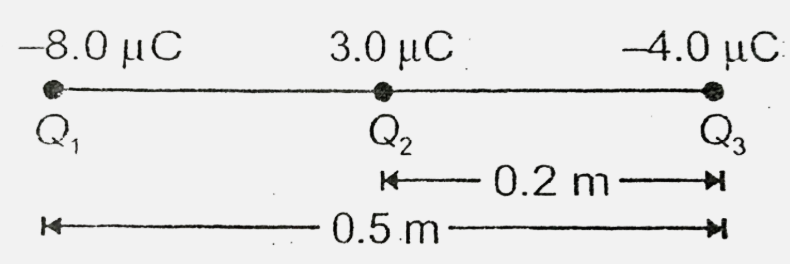
Strategy : The net force exerted on 3by particle 1 is the resultant of the force ¯¯¯¯¯F31 exerted on 3 by particle 1 and the force ¯¯¯¯¯F32 exerted on 3 by particle 2, ¯¯¯F=¯¯¯F31+¯¯¯F32
View SolutionIn fig. a central particle of charge −q is surrounded by two circular rings of charged particle of radii r and R, with Rgtr. what is the magnitude and dirction of the net electrostatic force on the central particle due to the other particles?

View SolutionSTATEMENT-1 : If a charge particle enters into a uniform electric field, then its path must be straight line.
and
STATEMENT -2 : Electrostatic force on a positive charge particle is always in the direction of electric field.
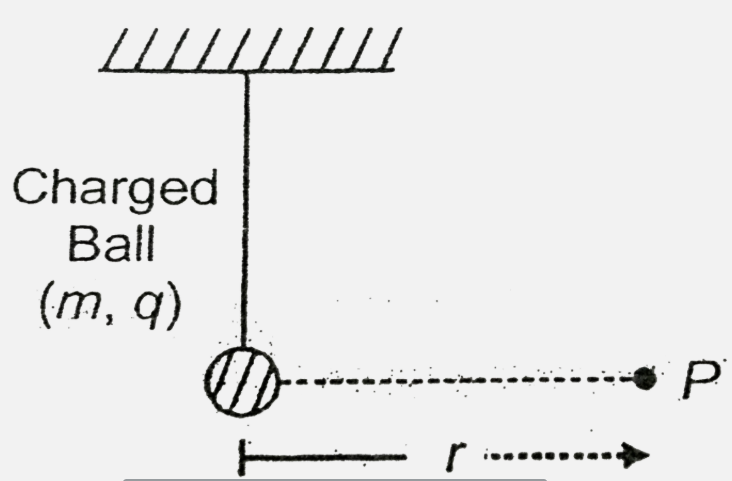
View SolutionThe electric field at point P due to a charged ball is given by
Ep=14πε0qr2
To measure 'E' at point P, A test charge q0 is placed at point P and measure electric force F upon the test charge. Check whether Fq0 is equal to 14πε0qr2 or not .
View SolutionA point charge +Q is placed at the centroid of an equilateral triangle. When a second charge +Q is placed at a vertex of the triangle, the magnitude of the electrostatic force on the central charge is 8 N. The magnitude of the net force on the central charge when a third charge +Q is placed at another vertex of the triangle is
View Solution
A charge particle q of mass is placed at a distance d from another charge particle -2q of mass 2 m in a uniform magnetic field B as shown if particle are projected towareds each other with equal speed v0, so that the two particle touches each other without collision during its motion (Assume only force due to magnetic field acts on the particle)
View Solution
