At time t = 0 second, voltage of an A.C. Generator starts from 0V and becomes 2V at time t=1100π second. The voltage keeps on increasing up 100 V, after wihich it starts to decrease. Find the frequency of the Generator.
100 Hz
1 Hz
2 Hz
5 Hz
The correct Answer is:B
To find the frequency of the A.C. generator, we can follow these steps:
Step 1: Understand the A.C. Voltage Equation
The voltage produced by an A.C. generator can be expressed as:
E(t)=E0sin(ωt)
where:
- E(t) is the instantaneous voltage at time t,
- E0 is the maximum voltage (amplitude),
- ω is the angular frequency in radians per second.
Step 2: Identify Given Values
From the problem, we know:
- At t=0 seconds, E(0)=0 V.
- At t=1100π seconds, E(1100π)=2 V.
- The maximum voltage E0=100 V.
Step 3: Substitute Known Values into the Voltage Equation
Substituting the known values into the voltage equation:
2=100sin(ω⋅1100π)
Step 4: Simplify the Equation
Dividing both sides by 100:
sin(ω⋅1100π)=2100=0.02
Step 5: Use Small Angle Approximation
Since ωt is small (as t=1100π is small), we can use the small angle approximation:
sin(x)≈x
Thus, we can write:
ω⋅1100π≈0.02
Step 6: Solve for Angular Frequency ω
Rearranging the equation gives:
ω≈0.02⋅100π
ω≈2π
Step 7: Find the Frequency f
The relationship between angular frequency ω and frequency f is given by:
ω=2πf
Substituting the value of ω:
2π=2πf
Dividing both sides by 2π:
f=1 Hz
Conclusion
The frequency of the A.C. generator is:
1 Hz
---
The voltage produced by an A.C. generator can be expressed as:
E(t)=E0sin(ωt)
where:
- E(t) is the instantaneous voltage at time t,
- E0 is the maximum voltage (amplitude),
- ω is the angular frequency in radians per second.
From the problem, we know:
- At t=0 seconds, E(0)=0 V.
- At t=1100π seconds, E(1100π)=2 V.
- The maximum voltage E0=100 V.
Substituting the known values into the voltage equation:
2=100sin(ω⋅1100π)
Dividing both sides by 100:
sin(ω⋅1100π)=2100=0.02
Since ωt is small (as t=1100π is small), we can use the small angle approximation:
sin(x)≈x
Thus, we can write:
ω⋅1100π≈0.02
Rearranging the equation gives:
ω≈0.02⋅100π
ω≈2π
The relationship between angular frequency ω and frequency f is given by:
ω=2πf
Substituting the value of ω:
2π=2πf
Dividing both sides by 2π:
f=1 Hz
The frequency of the A.C. generator is:
1 Hz
Similar Questions
A generator produces a time varying voltage given by V=240sin120t, where t is in second. The rms voltage and frequency are
View SolutionThe voltage of an a.c. source varies with time according to relation
E=120 sin 100πtcos100πt then
View SolutionAn A.C. generator generating an e.m.f. of ε=300sin(100πt)V is connected to a series combination of 16μF capacitor, 1H inductor and 100Ω resistor. Calculate
Resonant frequency fo
View SolutionThe voltage of an AC source varies with time according to the equation,V=100sin100πIcos100πt.Where t is in second and V is in volt.Then:
View SolutionThe voltage of an AC source varies with time according to the relation: E=120sin100πtcos100πtV. What is the peak voltage of the source?
View SolutionAn A.C. generator generating an e.m.f. of ε=300sin(100πt)V is connected to a series combination of 16μF capacitor, 1H inductor and 100Ω resistor. Calculate
Impedance of the circuit at the given frequency
View SolutionA body starts from rest and acquires velocity V in time T. The instantaneous power delivered to the body in time 't' proportional to
View SolutionIn the given circuit, one of the capacitors was connected to a voltage V0 and then at the moment t=0 was shorted by means of the switch. Find the amount of heat generated.
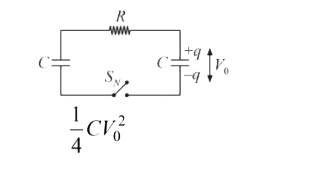
View SolutionIn the given circuit, one of the capacitors was connected to a voltage V0 and then at the moment t=0 was shorted by means of the switch. Find the amount of heat generated.

View SolutionIf the voltage in an ac circuit is reparesented by the equation V=220√2sin(314t−ϕ), calculate
frequency of ac
View Solution
