Which of the following statement(s) is/are TRUE?
I. Highest common factor of (32002−1) and (32002+1) is 4
II.(484−1) is exactly divisivle by 5
निम्नलिखित में से कौन सा/से कथन सत्य है?
I. (32002−1) तथा (32002+1) का महत्त्म
समापवर्तक 4 है ।
II.(484−1) 5 से पूर्णतः विभाजित है।
A. Only I/केवल I
B. Only II/केवल II
C. Neither I nor II/ न तो I न ही II
D. Both I and II/I तथा II दोनों
To solve the problem, we need to evaluate the two statements provided and determine their truthfulness.
Step 1: Evaluate Statement I
Statement I: The highest common factor (HCF) of 32002−1 and 32002+1 is 4.
To find the HCF of 32002−1 and 32002+1, we can use the property that:
HCF(a−b,a+b)=HCF(a2−b2,a+b)
In our case, let a=32002 and b=1. Thus, we have:
HCF(32002−1,32002+1)=HCF((32002)2−12,32002+1)
This simplifies to:
HCF(34004−1,32002+1)
Now, we can also note that 32002−1 is even (since any power of an odd number minus 1 is even) and 32002+1 is also even. Therefore, the HCF must be at least 2.
Next, we can check the divisibility by 4:
- 32002−1≡0mod4 (since 3≡−1mod4)
- 32002+1≡2mod4
Thus, the HCF is actually 2, not 4.
Conclusion for Statement I: False.
Step 2: Evaluate Statement II
Statement II: 484−1 is exactly divisible by 5.
To check this, we can use Fermat's Little Theorem, which states that if p is a prime and a is not divisible by p, then:
ap−1≡1modp
Here, let a=4 and p=5. According to Fermat's theorem:
44≡1mod5
Now, we need to find 484mod5:
84mod4=0(since 84=4×21)
Thus,
484≡(44)21≡121≡1mod5
Now, substituting this back into our expression:
484−1≡1−1≡0mod5
This shows that 484−1 is divisible by 5.
Conclusion for Statement II: True.
Final Conclusion
- Statement I is False.
- Statement II is True.
Statement I: The highest common factor (HCF) of 32002−1 and 32002+1 is 4.
HCF(a−b,a+b)=HCF(a2−b2,a+b)
In our case, let a=32002 and b=1. Thus, we have:
HCF(32002−1,32002+1)=HCF((32002)2−12,32002+1)
This simplifies to:
HCF(34004−1,32002+1)
Now, we can also note that 32002−1 is even (since any power of an odd number minus 1 is even) and 32002+1 is also even. Therefore, the HCF must be at least 2.
- 32002−1≡0mod4 (since 3≡−1mod4)
- 32002+1≡2mod4
Statement II: 484−1 is exactly divisible by 5.
ap−1≡1modp
Here, let a=4 and p=5. According to Fermat's theorem:
44≡1mod5
Now, we need to find 484mod5:
84mod4=0(since 84=4×21)
Thus,
484≡(44)21≡121≡1mod5
Now, substituting this back into our expression:
484−1≡1−1≡0mod5
This shows that 484−1 is divisible by 5.
- Statement I is False.
- Statement II is True.
Topper's Solved these Questions
Similar Questions
Which of the following statements is true ?
निम्नलिखित में से कौन सा कथन सत्य है?
View SolutionWhich of the following statement(s) is/are true?
I. 199+299+399+499+599 is excatly divisible by 5.
II. 3111>1714
निम्नलिखित में से कौन सा/से कथन सत्य है?
I. 199+299+399+499+599 5 से पूर्णत: विभाजित है।
II. 3111>1714
View Solution
Knowledge Check
[Co(CN)6]3− के बारे में निम्नलिखित में से कौन सा कथन सत्य है
A[Co(CN)6]3− में चार अयुग्मित इलेक्ट्रॉन उपस्थित होते हैं और यह एक निम्न चक्रण विन्यास में होगा।B[Co(CN)6]3− में चार अयुग्मित इलेक्ट्रॉन उपस्थित होते हैं और यह एक उच्च चक्रण विन्यास में होगा।C[Co(CN)6]3− में अयुग्मित इलेक्ट्रॉन उपस्थित नहीं होते हैं और यह एक उच्च चक्रण विन्यास में होगा।D[Co(CN)6]3− में अयुग्मित इलेक्ट्रॉन उपस्थित नहीं होते हैंनिम्नलिखित में से कौन सा SN1 के प्रति सबसे कम अभिक्रियाशील है?
A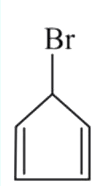 B
B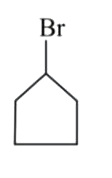 C
C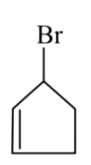 D
D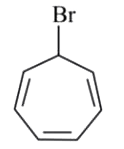
निम्नलिखित में से कौन सा रेखाचित्र एक समभारिक के लिए है: (दिया गया है: nRP>1 )
A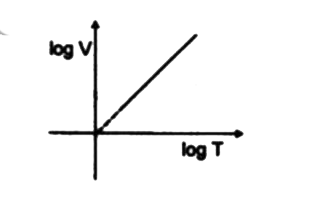 B
B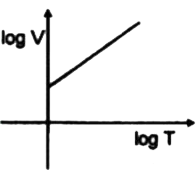 C
C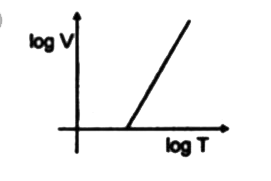 D
D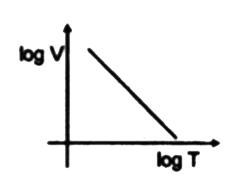
Which of the following options is divisible by 3?
निम्नलिखित में से कौन सा विकल्प 3 से विभाज्य है?
View SolutionWhich of the follwing statement (s) is/are TRUE?
निम्नलिखित में से कौन सा/से कथन सत्य है/हैं?
I. 333>333
II. 333>(33)3
View SolutionWhich of the following numbers is divided by 3?
निम्नलिखित में से कौन सी संख्या 3 से विभाजित है?
View SolutionWhich of the following statement(s) is/are true?
निम्नलिखित में से कौन सा/से कथन सत्य है?
I. 123+234+345>8
II. 612−534+414>5
View Solutionनिम्नलिखित में से कौन सा यौगिक (S)-4-क्लोरो-1 मेथिलसाइक्लोहेक्सीन
View Solution
