The number of triangles that the four lines y=x+3,y=2x+3,y=3x+2, and y+x=3 form is (a) 4 (b) 2 (c) 3 (d) 1Solution in Tamil
4
2
3
1
The correct Answer is:C
The lines y=x+3, y=2x+3 and y+x=3 are concurrent at (0,3).
Rough sketch of the lines is as shown in the figure.
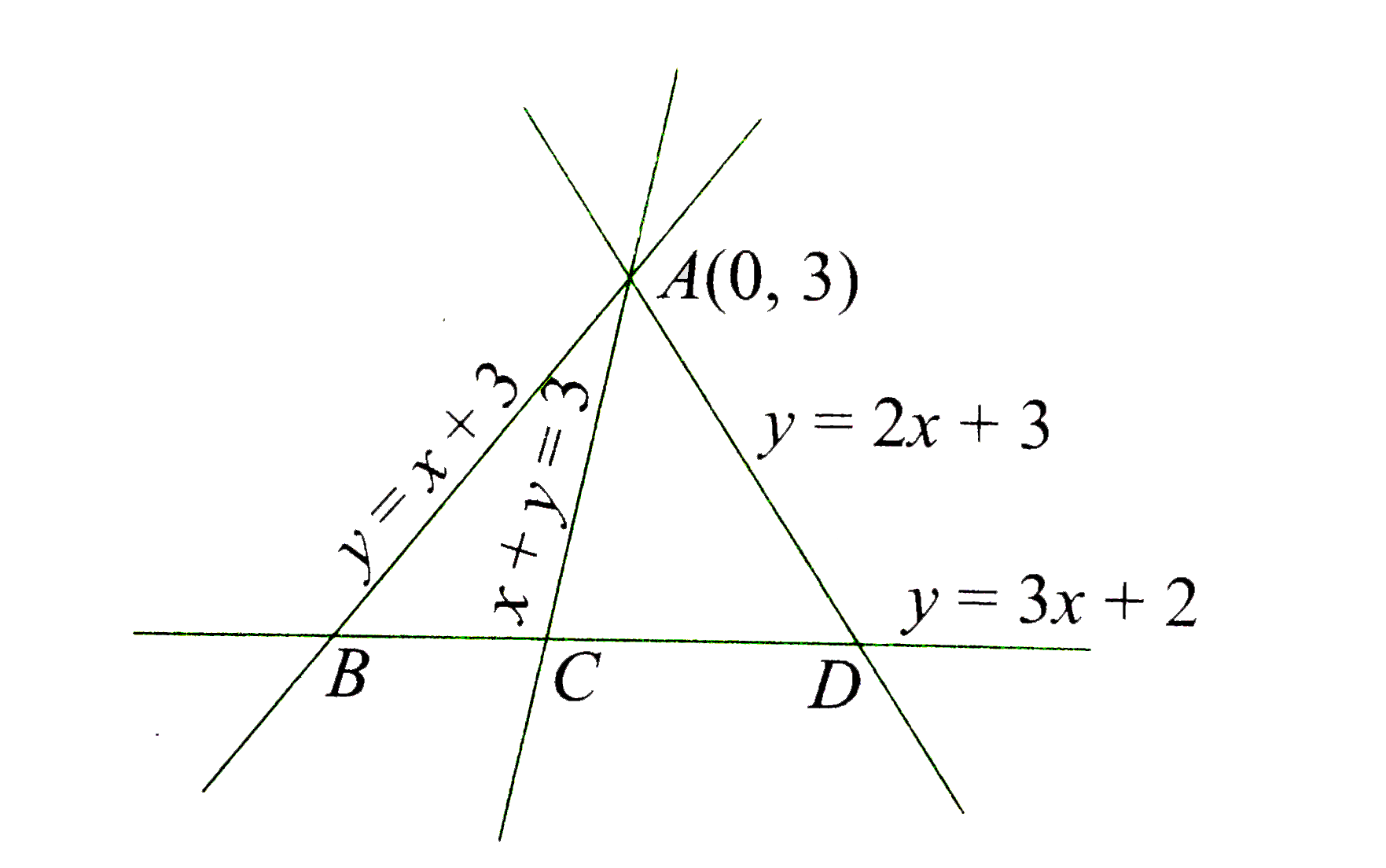
From the figure, three triangles ABD, ABC nad ACD can be formed.
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Multiple)
Explore 30 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Comprehension)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise 2.6
Explore 5 Videos
- STRAIGHT LINEBook:CENGAGEChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 3 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:JEE Advanced Previous Year
Explore 1 Video
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionLet L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
Area enclosed by the line L and the coordinate axes is
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionIf (a, b) be an end of a diagonal of a square and the other diagonal has the equation x−y=a, then another vertex of the square can be
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0 is ________
View SolutionIf y3−y=2x,then(x2−127)d2ydx2+xdyd= y b. y3 c. y9 d. y27
View SolutionThe number of triangles that the four lines y = x + 3, y = 2x + 3, y = 3x + 2, and y + x = 3 form is (a) 4 (b) 2 (c) 3 (d) 1
View SolutionIf [2x+y4x5x−74x]=[77y−13yx+6] , then the value of x+y is x=3 , y=1 (b) x=2 , y=3 (c) x=2 , y=4 (d) x=3 , y=3
View SolutionWhich of the following line is passing through point of intersection of line x−42=y−32=z−51 and the plane x+y+z=2 (a) x2=y+13=z−34 (b) x−23=y−13=z−32 (c) x2=y+13=z−24 (d) x−22=y+13=z+34
View SolutionThe locus of the centre of the circle passing through (1,1) and cutting x2+y2=4 orthogonally is : (A) x+y=3 (B) x+2y=3 (C) 2x+y=3 (D) 2x−y=3
View Solution(a) Draw the graph for line y=3x.
(b) y=-x
(c) y=2x +4
(d) y=-x+2
(e) y=2x-4
View SolutionThe number of triangles that the four lines y=x+3,y=2x+3,y=3x+2, and y+x=3 form is (a) 4 (b) 2 (c) 3 (d) 1
View SolutionThe solution of x2+y2dydx=4 is
a. x2+y2=12x+C b. x2+y2=3x+C c. x3+y3=3x+C d. x3+y3=12x+C
View SolutionWhich of the following line is passing through point of intersection of line x−42=y−32=z−51 and the plane x+y+z=2 (a) x2=y+13=z−34 (b) x−23=y−13=z−32 (c) x2=y+13=z−24 (d) x−22=y+13=z+34
View SolutionTwo numbers x and y such that x + y=2 and x3y is maximum, are...... A) 1/3, 5/3 B) 3/2, 1/2 C) 1, 1 D) 6/5, 4/5
View Solutionx3−3x2y+y2x−y3 में से 2x3−y3 को घटाइए
View Solution
