Prove that sin(cot−1(tan(cos−1x)))=x,x>0Solution in Tamil
For θ=cos−1x, we have the following triangle

∴E=sin(cot−1(tan(cos−1x)))
=sin(cot−1(tan(tan−1.√1−x2x)))
=sin(cot−1.√1−x2x)
Now, for α=cot−1(√1−x2)x, we have following triangle
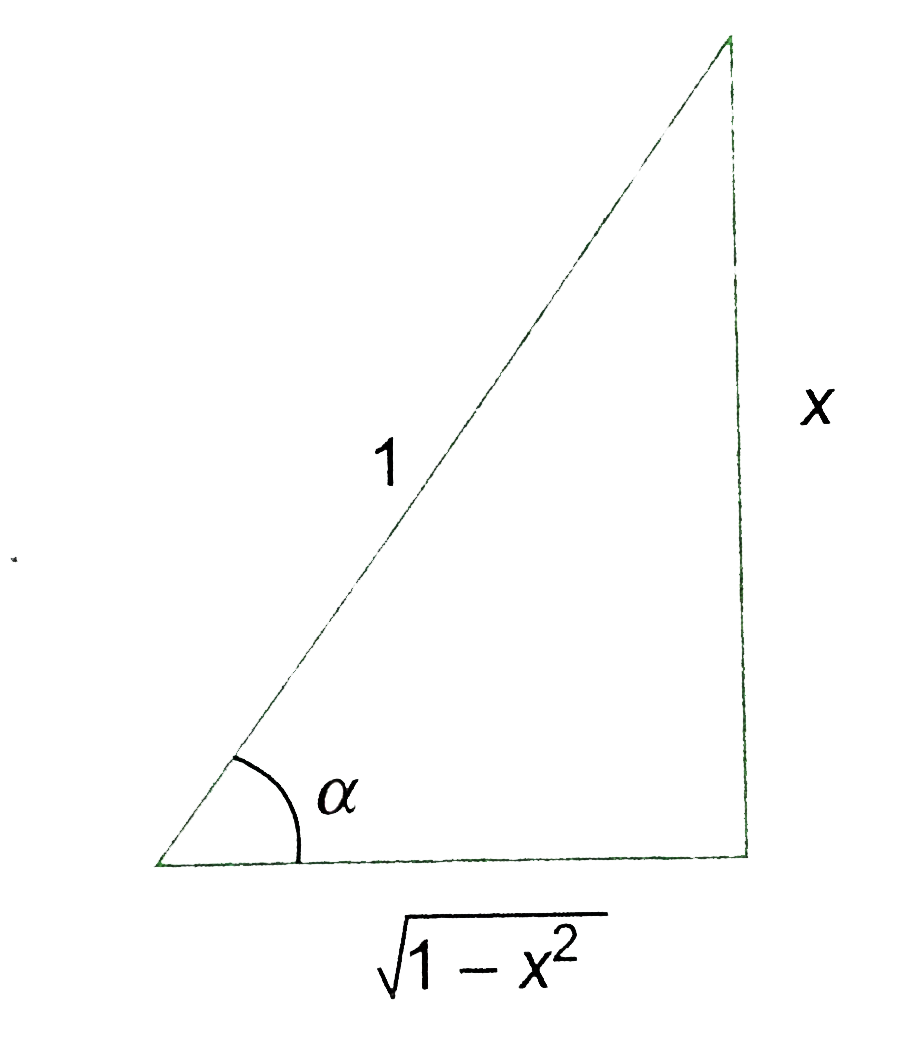
∴E=sin(sin−1.x1)=x
টপার এই প্রশ্নগুলো সমাধান করেছে
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.1
12 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.2
6 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Question Bank
7 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - JEE Previous Year
15 Videos
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
সম্পর্কিত প্রশ্ন
Find the principal value of (a) cosec−1(−1) (b) cot−1(−1√3)
View SolutionFind the value of tan−1(−tan.13π8)+cot−1(−cot(19π8))
View SolutionIf α and β are the two zeroes of the equation 3cos−1(x2−5x−112)=π, then (α3+β3) equals
View SolutionFind the values of λ such that x,y,z≠(0,0,0)and(ˆi+ˆj+3ˆk)x+(3ˆi−3ˆj+ˆk)y+(−4ˆi+5ˆj)z=λ(xˆi+yˆj+zˆk),whereˆi,ˆjandˆk are unit vector along coordinate axes.
View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
View SolutionSimplify sincot−1tancos−1x,x>0
View SolutionProve that : sincot−1tancos−1x=x
View SolutionProve that sin(cot−1(tan(cos−1x)))=x,x>0
View SolutionProve that sincot−1tancos−1x=sincosec−1cottan−1x=x, where x∈[0,1]
View SolutionWhat is sin [cot−1{cos(tan−1x)] where x > 0, equal to ?
View Solutionsin[cot−1{cos(tan−1x)}], जहाँ x>0, का मान किसके बराबर है ?
View Solutionसिद्ध करे कि
sincot−1tancos−1x=x.
View Solutionसिद्ध कीजिए :
sin[cot−1{tan(cos−1−x)}]=x
View Solutionsincot−1cos(tan−1x)=√x2+1x2+2(x>0)
View SolutionIf x>0, then the value of sin[cot−1cos(tan−1x)] is equal to -
View Solutionसिद्ध कीजिए कि -
sin[cot−1{(tan(cos−1x)}]=x.
View Solution

