
Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
The value of α for which side of nth square equal to the diagonal of (n+1)th square isSolution in Tamil
13
14
12
1√2
The correct Answer is:C
(c) 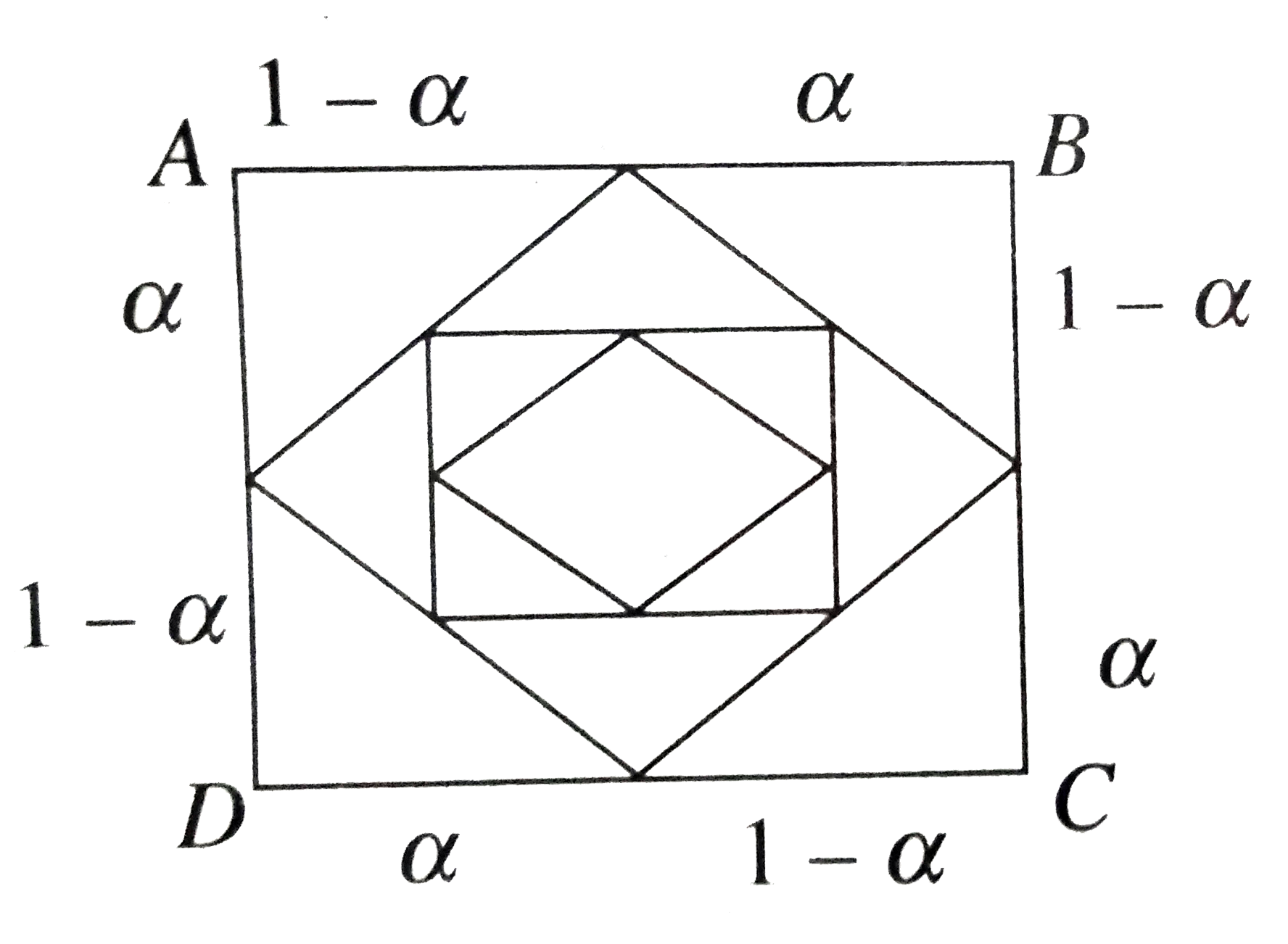
Clearly from the diagram,
a1=1
(an+1)2=[(1−α)2+α2](an)2⇒An+1=[2α2−2α+1]An
For α=13, (an+1)2=59(an)2
⇒An+1An=59
⇒A2=59, A3=(59)2,...
⇒An=(59)n−1
An<110⇒(59)n−1<110
⇒ Least value of n is 5.
∞∑n=1An=83
⇒11−(2α2−2α+1)=83
⇒16α2−16α+3=0
⇒16α2−12α−4α+3=0
⇒(4α−1)(4α−3)=0
⇒α=14, 34
The side of nth square equal to the diagonal of (n+1)th square. ⇒√2an=an+1
⇒(an+1)2(an)2=12
⇒4α2−4α+1=0
⇒α=1/2
Topper's Solved these Questions
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - Multiple Correct Answer
4 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - Examples
113 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Video
- PROBABILITY IIBOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - NUMARICAL VALUE TYPE
2 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - JEE Advanced Previous Year
11 Videos
Similar Questions
If a,x, and b and b are in A.P .., a,y , and a,z,b are in H.P such that x=9z and a>0,b>0 then
View SolutionWrite down the sequence whose nth term is 2n/n and (ii) [3+(−1)n]/3n
View SolutionIt is given that in a group of 4 students, the probability of 2 students not having the same birthday is 0.893. What is the probability that the 2 students have the same birthday?
View SolutionOf the three independent event E1,E2 and E3, the probability that only E1 occurs is α, only E2 occurs is β and only E3 occurs is γ. If the probavvility p that none of events E1,E2 or E3 occurs satisfy the equations (α−2β)p=αβ and (β−3γ)p=2βγ. All the given probabilities are assumed to lie in the interval (0, 1). Then, probability of occurrence of E1probability of occurrence of E3 is equal to
View SolutionLet ABC be a triangle such that ∠ACB=π6 and let a,bandc denote the lengths of the side opposite to A,B,andC respectively. The value(s) of x for which a=x2+x+1,b=x2−1,andc=2x+1 is(are) −(2+√3) (b) 1+√3 2+√3 (d) 4√3
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionIf the figure given below ( not to scale), ABCD, CBEF and EGHF are three congruent squares. Find ∠FAE+∠HAG.
View SolutionWhat is the distance OA for the square shown in figure :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_015_Q01.png" width="80%"gt
View SolutionA square lies above the X - axis and has one vertex at the origin . The side passing through the origin makes an angle α(o<α<π/4) with the positive direction of the X - axis . Prove that the equation of its diagonals are ,
y(cosα−sinα)=x(sinα+cosα) ,
and y(sinα+cosα)+x(cosα−sinα)=a
where , is the length of each side of the square
View SolutionIf each of sides of the square ABCD be a cm, then the length of each of the sides of the square, formed by joining the mid-points of the sides of ABCD is
View Solutionimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/CEN_ALG_DPP_4_2_E01_231_Q01.png" width="80%"gt
Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
Ifα=13, then the least value of n for which An>110 is
View Solution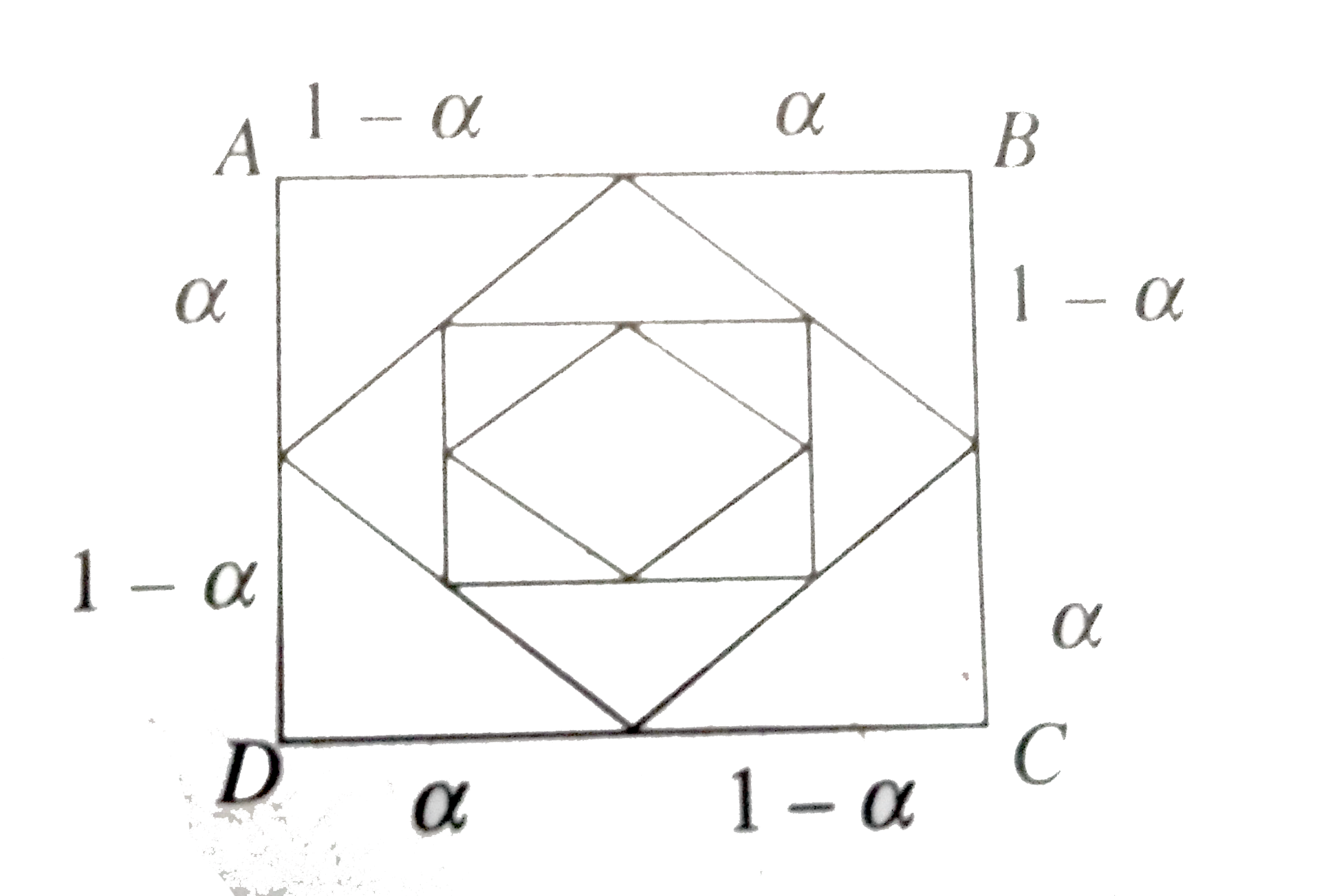
Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
The value of α for which ∞∑n=1An=83 is/are
View Solution Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
The value of α for which side of nth square equal to the diagonal of (n+1)th square is
View SolutionOne side of a square makes an angle α with x axis and one vertex of the square is at origin. Prove that the equations of its diagonals are x(sinα+cosα)=y(cosα−sinα) or x(cosα−sinα)+y(sinα+cosα)=a, where a is the length of the side of the square.
View Solution

