Refer to the following diagram :

Column IColumn IIa.Collinear vectorsp.→ab.Coinitial vectorsq.→bc.Equal vectorsr.→cd.Unlike vectors (same initial point)s.→dSolution in Tamil
The correct Answer is:2
(q) cosx+cosy+cosz=0andsinx+siny+sinz=0
cosx+cosy=−cosz …(1)
and sinx+siny=−sinz …(2)
Squaring and adding we get,
1+1+2(cosxcosy+sinxsiny)=1
⇒2+2cos(x−y)=1
⇒2cos(x−y)=−1
⇒cos(x−y)=−12
⇒2cos2(x−y2)−1=−12
⇒cos(x−y2)=12
(r) cos(π4−x)cos2x+sinxsin2xsecx
=cosxsin2xsecx+cos(π4+x)cos2x
⇒[cos(π4−x)−cos(π4+x)]cos2x
=(cosxsin2xsecx−sinxsin2xsecx)
⇒2√2sinxcos2x=(cosx−sinx)sin2xsecx
⇒√2sinxcos2x=(cosx−sinx)2sinx
⇒1√2=1cosx+sinx
⇒x=π4
⇒secx=secπ4=√2
Topper's Solved these Questions
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBook:CENGAGEChapter:TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASExercise:JEE Advanced Previous Year
Explore 5 Videos
- TRIGONOMETRIC FUNCTIONS Book:CENGAGEChapter:TRIGONOMETRIC FUNCTIONS Exercise:SINGLE CORRECT ANSWER TYPE
Explore 37 Videos
- TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS Book:CENGAGEChapter:TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS Exercise:Multiple Correct Answers Type
Explore 6 Videos
Similar Questions
The value of 13∑k=11sin(π4+(k−1)π6)sin(π4+kπ6) is equal to
View SolutionThe circular wire of diameter 10 cm is cut and placed along the circumference of a circle of diameter 1 meter. The angle subtended by the wire at the centre of circle is equal to
View SolutionIf sec x + tan x =22/7 , find the value of tanx/2
View SolutionColumn I, Column II Collinear vectors, p.→a Coinitial vectors, q. →b Equal vectors, r. →c Unlike vectors (same intitial point), s. →d
View SolutionColumn-I show vector diagram relating three vectors →a,→b and →c. Match the vector equation in column -II, with vector diagram in column-I:
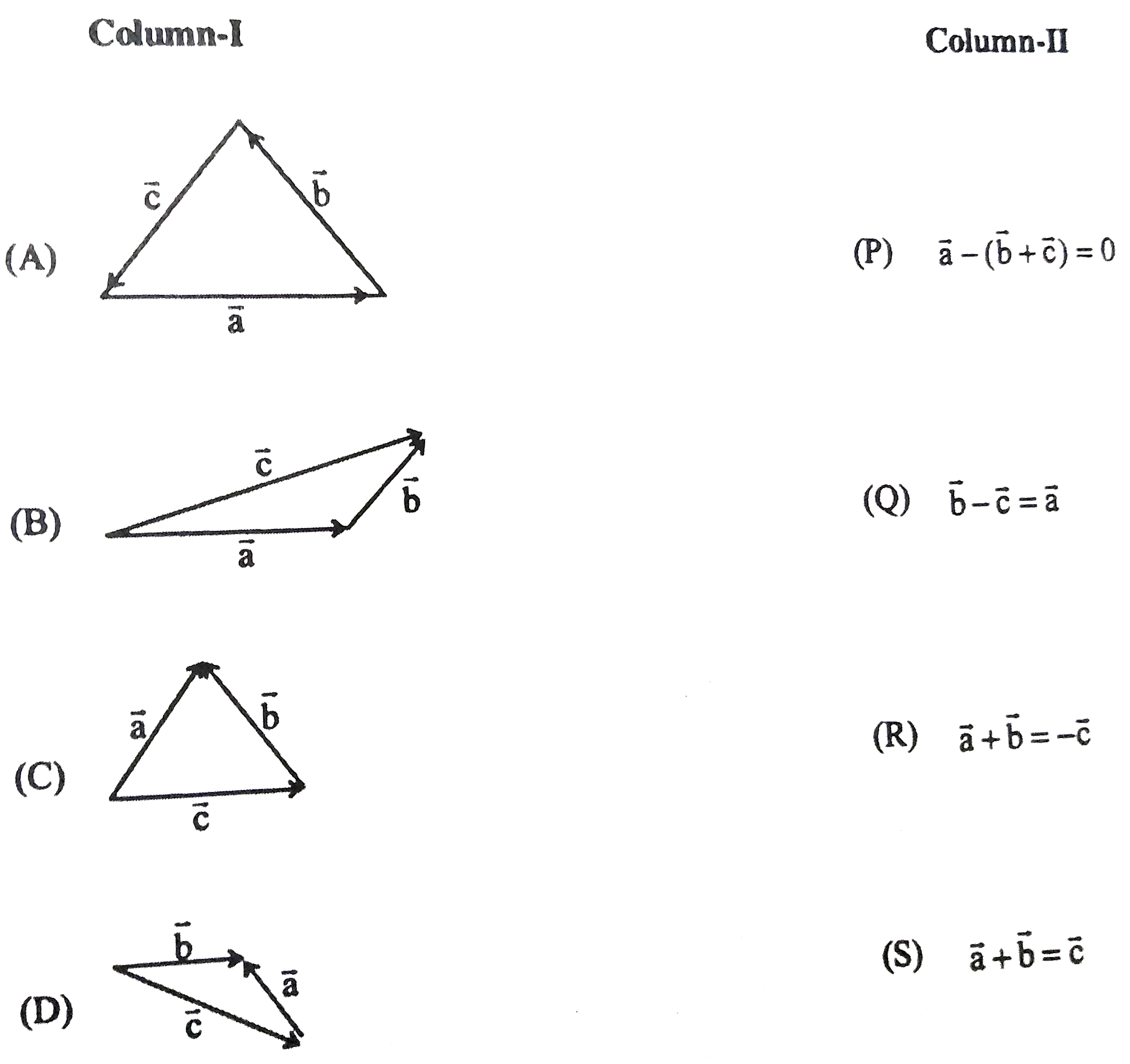
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionFigure shows three vectors →a,→b and →c. If ¯¯¯¯¯¯RQ=2¯¯¯¯¯¯PR, which of the following relation is correct :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R01_E02_013_Q01.png" width="80%"gt
View SolutionWrite the vector →F in terms of its component :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R02_E02_002_Q01.png" width="80%"gt
View SolutionMatch the followings (column I with column II)
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C03_E01_011_Q01.png" width="80%"gt
View SolutionMatch the terms in column I with those in column II: ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C07_E01_011_Q01.png" width="80%"gt
View SolutionMatch column I with column II
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C16_E01_002_Q01.png" width="80%"gt
View SolutionMatch column I with column II:
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C18_E01_003_Q01.png" width="80%"gt
View SolutionMatch the items of column I with those of column II: ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C19_E01_011_S01.png" width="80%"gt
View SolutionMatch Column I with Column II: ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C20_E01_010_Q01.png" width="80%"gt
View Solution
