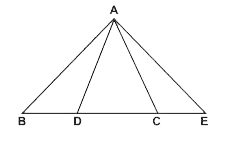
In △ABC, AD is the median and G is a point on AD such that AG : GD = 2 : 1, then ar(△BDG):(△ABC) is equal to :
त्रिभुज ABC में, AD माध्यिका है तथा
G, AD पर ऐसा बिंदु है कि AG : GD = 2 : 1 है, तो ar(△BDG):(△ABC) का मान ज्ञात करें |
1:4
1:9
1:6
1:3
To solve the problem, we need to find the ratio of the area of triangle BDG to the area of triangle ABC, given that AD is the median and point G divides AD in the ratio 2:1.
1. Understanding the Median:
- In triangle ABC, AD is the median. This means that D is the midpoint of side BC. Therefore, BD = DC.
2. Identifying the Centroid:
- The centroid (G) of triangle ABC divides each median in the ratio 2:1. Since AG:GD = 2:1, point G divides median AD into two segments where AG is twice as long as GD.
3. Area Division by Medians:
- A property of medians in a triangle is that they divide the triangle into 6 smaller triangles of equal area. This means that the area of triangle ABC is divided into 6 equal parts by the medians.
4. Finding the Area of Triangle BDG:
- Triangle BDG is one of these smaller triangles formed by the median AD and the line segment BD. Since the area of triangle ABC is divided into 6 equal parts, the area of triangle BDG is equal to the area of one of these parts.
5. Calculating the Ratio:
- The area of triangle BDG is 1 part out of the total 6 parts of triangle ABC. Therefore, the ratio of the area of triangle BDG to the area of triangle ABC is:
ar(△BDG):ar(△ABC)=1:6
Final Answer:
The ratio of the area of triangle BDG to the area of triangle ABC is 16 or 1:6.
---
- In triangle ABC, AD is the median. This means that D is the midpoint of side BC. Therefore, BD = DC.
- The centroid (G) of triangle ABC divides each median in the ratio 2:1. Since AG:GD = 2:1, point G divides median AD into two segments where AG is twice as long as GD.
- A property of medians in a triangle is that they divide the triangle into 6 smaller triangles of equal area. This means that the area of triangle ABC is divided into 6 equal parts by the medians.
- Triangle BDG is one of these smaller triangles formed by the median AD and the line segment BD. Since the area of triangle ABC is divided into 6 equal parts, the area of triangle BDG is equal to the area of one of these parts.
- The area of triangle BDG is 1 part out of the total 6 parts of triangle ABC. Therefore, the ratio of the area of triangle BDG to the area of triangle ABC is:
ar(△BDG):ar(△ABC)=1:6
The ratio of the area of triangle BDG to the area of triangle ABC is 16 or 1:6.
टॉपर्स ने हल किए ये सवाल
समान प्रश्न
After giving two successive discounts, each of x%, on the marked price of an article, total discount is Rs. 259.20. If the marked price of the article is Rs. 720, then the value of x is :
View SolutionThe product of HCF and LCM of two numbers is 3321. If one of the numbers is 369. The HCF of the number is
यदि दो संख्याओं के HCF और LCM का गुणनफल 3321 है।यदि इनमे से एक संख्या 369 है। तो HCF ज्ञात कीजिये?
View Solution(v) ΔABC is equilateral and AD is a median of it. If G be the centroid of ΔABCandGD=10cm. find the length of GB.
View SolutionIn the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
View SolutionIn triangle ABC , F and E are the points on sides AB and AC respectively, such that FE || BC and FE divides the triangle in two parts of equal area. If AD bot BC and AD intersect FE at G, then GD: AG = ? triangle ABC में F और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि FE || BC है तथा FE त्रिभुज को बराबर क्षेत्रफल वाले दो भागों में विभाजित करती है | यदि AD bot BC है और AD, FE को G पर काटती है, तो GD: AG = ?
View SolutionIn triangle ABC , AD is median and G is the point on AD such that AG: GD = 2: 1, then ar(triangle ABG) :ar(triangle ABC) is equal to : त्रिभुज ABC में, AD मध्यिका है तथा G, AD पर स्थित ऐसा बिंदु है कि AG: GD = 2 : 1 है, तो ar(triangle ABG) :ar(triangle ABC) का मान किसके बराबर होगा ?
View SolutionIn triangle ABC , AD is median and P is the point on AD such that AP : PD = 3 : 4, then ar(triangle APB) :ar(triangle ABC) is equal to : त्रिभुज ABC में, AD मध्यिका है तथा P, AD पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है, तो ar(triangle APB) :ar(triangle ABC) का मान किसके बराबर होगा ?
View SolutionIn triangle ABC ,AD is a median and P is a point on AD such that AP : PD = 3 : 4. Then ar (triangle BPD): ar (triangle ABC) is equal to: त्रिभुज ABC में, AD एक माध्यिका है और P, AB पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है| ar (triangle BPD): ar (triangle ABC) ज्ञात करें |
View SolutionIn triangle ABC ,P is a point on BC such that BP : PC = 1 : 2 and Q is the mid point of BP. then, ar(triangle ABQ) :ar (triangle ABC) is equal to: त्रिभुज ABC में, P, BC पर स्थित ऐसा बिंदु है कि BP : PC = 1 : 2 है और Q, BP का मध्य बिंदु है | तो ar(triangle ABQ) :ar (triangle ABC) का मान क्या होगा ?
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 3 : 4 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 3 : 4 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान ज्ञात करें |
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 4 : 3 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ACB) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 4 : 3 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ACB) का मान ज्ञात करें |
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 4:5 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 4:5 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान ज्ञात करें |
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 4 : 11 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 4 : 11 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान किसके बराबर होगा ?
View SolutionIn a △ABC, D and E are two points on the sides AB and BC , respectively such that AD : DB = 2: 3 and DE || AC. If the area of △ADE is equal to 18 square cm, then what is the area ( In square cm) of △ABC ?
किसी त्रिभुज ABC में, D और E क्रमश: भुजा AB और BC पर स्थित बिंदु हैं जो इस प्रकार हैं कि AD : DB = 2: 3 है तथा 9DE || AC है | यदि त्रिभुज ADE का क्षेत्रफल 18 वर्ग सेमी के बराबर है, तो त्रिभुज ABC का क्षेत्रफल ( वर्ग सेमी में ) ज्ञात करें
View SolutionD is the midpoint of BC of triangle ABC . Point E lies on AC such that CE = 1/3 AC . BE and AD intersect at G. What is (AG)/(GD) ? D त्रिभुज ABC का मध्य बिंदु है | बिंदु E, AC पर इस प्रकार स्थित है कि CE = 1/3 AC है| BE और AD एक-दूसरे को 9 पर प्रतिच्छेद करते हैं। (AG)/(GD) क्या है?
View Solution