A square has been inscribed in a circle. What is the ratio of the length of a side of the square to the radius of the circle ?
एक वर्ग किसी वृत्त के भीतर स्थित है | वर्ग की एक भुजा की लंबाई तथा वृत्त की त्रिज्या में अनुपात ज्ञात करें |
2:1
1:√2
1:2
√2:1
To find the ratio of the length of a side of a square (let's denote it as a) to the radius of the circle (denote it as r), we can follow these steps:
Step 1: Understanding the Geometry
When a square is inscribed in a circle, the corners of the square touch the circle. The center of the circle is also the center of the square.
Step 2: Identify the Relationship
Let’s denote the vertices of the square as A,B,C,D and the center of the circle as O. The radius of the circle is the distance from the center O to any vertex of the square, for example, OA.
Step 3: Using the Pythagorean Theorem
The diagonal of the square can be calculated using the Pythagorean theorem. The diagonal BD of the square can be expressed in terms of the side length a:
BD2=AB2+AD2=a2+a2=2a2
Thus,
BD=√2a2=a√2
Step 4: Relating the Diagonal to the Radius
The diagonal BD is also equal to the distance from the center O to the vertex A (which is the radius r). Therefore, we have:
BD=r√2
Equating the two expressions for BD:
a√2=r√2
Step 5: Solving for the Ratio
To find the ratio ar, we can rearrange the equation:
a=r
Thus, the ratio of the side length of the square to the radius of the circle is:
ar=1√2
Step 6: Simplifying the Ratio
We can express this ratio in a more standard form:
ar=√22
Final Answer
The ratio of the length of a side of the square to the radius of the circle is:
ar=1√2or√22
When a square is inscribed in a circle, the corners of the square touch the circle. The center of the circle is also the center of the square.
Let’s denote the vertices of the square as A,B,C,D and the center of the circle as O. The radius of the circle is the distance from the center O to any vertex of the square, for example, OA.
The diagonal of the square can be calculated using the Pythagorean theorem. The diagonal BD of the square can be expressed in terms of the side length a:
BD2=AB2+AD2=a2+a2=2a2
Thus,
BD=√2a2=a√2
The diagonal BD is also equal to the distance from the center O to the vertex A (which is the radius r). Therefore, we have:
BD=r√2
Equating the two expressions for BD:
a√2=r√2
To find the ratio ar, we can rearrange the equation:
a=r
Thus, the ratio of the side length of the square to the radius of the circle is:
ar=1√2
We can express this ratio in a more standard form:
ar=√22
The ratio of the length of a side of the square to the radius of the circle is:
ar=1√2or√22
Topper's Solved these Questions
Similar Questions
After giving two successive discounts, each of x%, on the marked price of an article, total discount is Rs. 259.20. If the marked price of the article is Rs. 720, then the value of x is :
View SolutionThe product of HCF and LCM of two numbers is 3321. If one of the numbers is 369. The HCF of the number is
यदि दो संख्याओं के HCF और LCM का गुणनफल 3321 है।यदि इनमे से एक संख्या 369 है। तो HCF ज्ञात कीजिये?
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View SolutionIn the given figure, ABCD is a square. EFGH is a square formed by joining mid points of sides of ABCD. LMNO is a square formed by joining mid points of sides of EFGH. A circle is inscribed inside EFGH. If area of circle is 38.5 cm2, then what is the area (in cm2) of square ABCD?
दी गई आकृति में, ABCD एक वर्ग है। ABCD की भुजाओं के केन्द्र बिन्दुओं को जोड़कर एक वर्ग EFGH बनाया गया हैं EFGH की भुजाओं के केन्द्र बिन्दुओं को जोड॒कर एक वर्ग LMNO बनाया गया है। एक वृत्त को वर्ग EFGH में अंकित किया गया हैं यदि वृत्त का क्षेत्रफल 38.5 से.मी.2 है, तो वर्ग ABCD का क्षेत्रफल (से.मी.2 में) क्या है?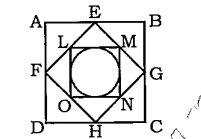
View SolutionAn equilateral triangle ABC is insribed in a circle as shown figure. A square of largest possible area is made inside this triangle as shown. Another circle made inscribing the square. What is the ratio of area of large circle and the small circle? जैसा की आकृति में दर्शाया गया है, एक समबाहु त्रिभुज ABC एक वृत्त में बनाया गया है। जैसा दर्शाया गया है, सबसे बड़े संभावित क्षेत्रफल वाला वर्ग इस त्रिभुज के अंदर बनाया गया है। बड़े वृत्त तथा छोटे वृत्त के क्षेत्रफल का अनुपात क्या है?
View SolutionThe area of a circle and a square are same. The ratio of the diagonal of the square to the radius of the circle is- एक वृत्त और एक वर्ग का क्षेत्रफल एकसमान है। वर्ग की विकर्ण और वृत्त की त्रिज्या का अनुपात क्या होगा?
View Solutionएक बिंदु की शक्ति | किसी अन्य वृत्त के सापेक्ष दिए गए वृत्त की स्थिति
View SolutionThe side of a square is 6 cm. Find the area of the largest circle that can be drawn inside the square. (π=227)
एक वर्ग की भुजा 6 cm है | वर्ग के अंदर बनने वाले सबसे बड़े वृत्त का क्षेत्रफल कितना है?
View SolutionWhat is the area of the largest circle that can be inscribed in a square of side 28 cm? (Take π=227)
उस सबसे बड़े वृत्त का क्षेत्रफल ज्ञात करें जिसे 28 सेमी भुजा वाले एक वर्ग के भीतर खींचा जा सकता है |
View SolutionIf the length of a side of a square is equal to the diameter of a circle, then the ratio between the areas of square and circle is (π=227)
यदि किसी वर्ग की भुजा की लम्बाई किसी वृत्त के व्यास के बराबर है, तब वर्ग तथा वृत्त के क्षेत्रफल का अनुपात हैः
View SolutionThe area of a square and rectangle are equal. The length of the rectangle is greater than the length of a side of the square by 10cm and the breadth is less than 5cm. The perimeter (in cm ) of the rectangle is: एक वर्ग और आयत का क्षेत्रफल बराबर होता है। आयत की लंबाई वर्ग के एक भुजा की लंबाई से 10 सेमी अधिक और चौड़ाई 5 सेमी कम है। आयत की परिमाप (सेमी में) ज्ञात करे:
View SolutionAB and CD are two parallel chords of a circle such that AB = 6 cm and CD = 2AB. Both chords are on the same side of the centre of the circle. If the distance between is equal to one-fourth of the length of CD, then the radius of the circle is- AB और CD किसी वृत्त की दो ऐसी समानांतर जीवाएं है कि AB = 6 सेमी है और CD = 2AB है | दोनों जीवाएं वृत्त के केंद्र के एक ही तरफ हैं | यदि बीच की दूरी CD की लंबाई के एक चौथाई के बराबर है, तो वृत्त की त्रिज्या ज्ञात करें |
View SolutionAB is a diameter of a circle with centre O. CB is a tangent to the circle at B. AC intersects the circle at G. If the radius of the circle is 6cm and AG = 8cm, then the length of BC is : AB एक वृत्त का व्यास है जिसका केंद्र O है | CB, B पर वृत्त की स्पर्श रेखा है| AC, वृत्त को G पर काटता है | यदि वृत्त की त्रिज्या 6 सेमी है तथा AG = 8 सेमी है, तो BC की लंबाई ज्ञात करें |
View SolutionIn a circle of radius 13 cm , a chord is at a distance of 12 cm from the centre of the circle. What is the length of the chord?
13 सेमी त्रिज्या वाले एक वृत्त में, वृत्त के केंद्र से 12 सेमी की दूरी पर एक जीवा है | जीवा की लंबाई ज्ञात करें |
View SolutionIn a circle of radius 17 cm, a chord is at a distance of 15 cm from the centre of the circle. What is the length of the chord?
17 सेमी त्रिज्या वाले एक वृत्त में, वृत्त के केंद्र से 15 सेमी की टूरी पर एक जीवा है| जीवा की लंबाई ज्ञात करें |
View Solution
