Suppose the cubic x3−px+q has three distinct real roots, where p>0 and q>0. Then which one of the following holds?Solution in Gujrati
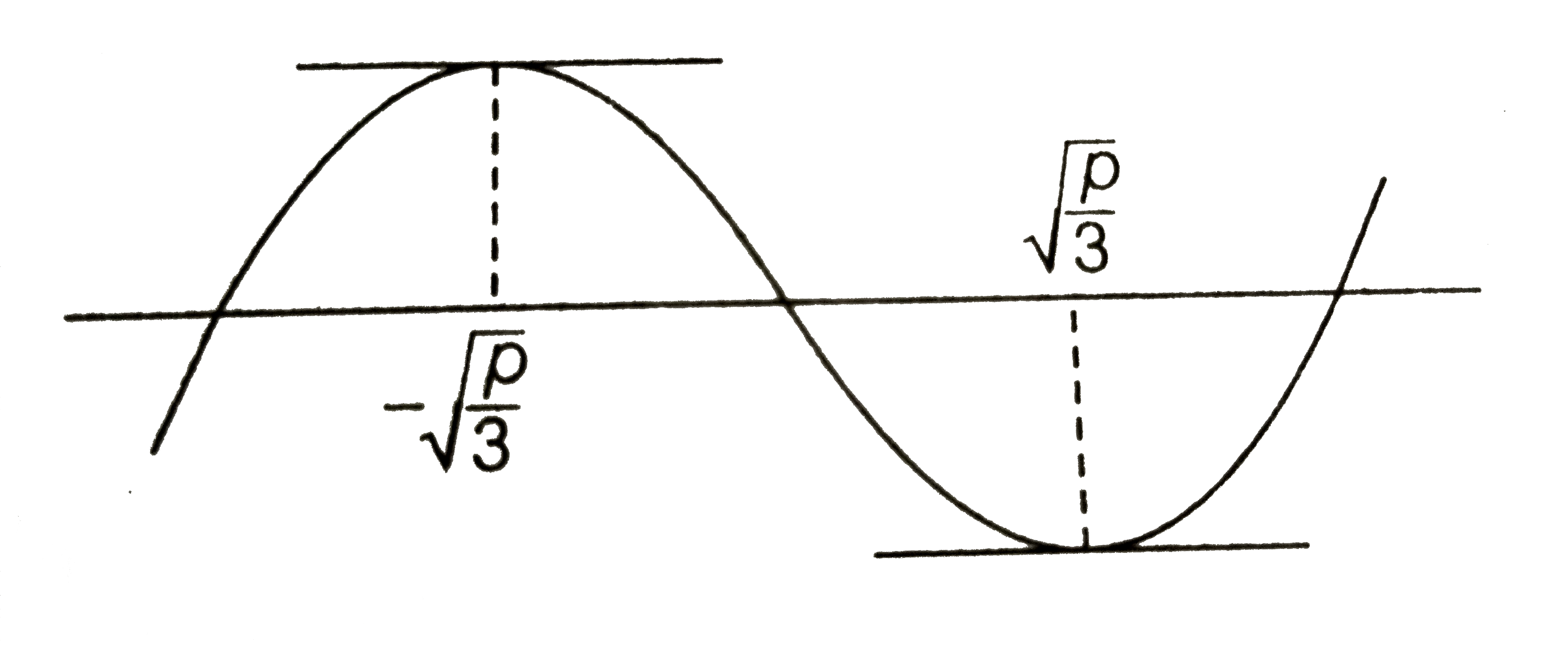
The cubic has minima at (−√p3) and maxima at √p3
The cubic has minima at both √p3 and (−√p3)
The cubic has maxima at both √p3 and (−√p3)
The cubic has minima at √p3 and maxima at (−√p3)
The correct Answer is:C
Let f(x)=x3−px+q
∴f'(x)=3x2−p
⇒f''(x)=6x
For maxima or minima f'(x)=0
∴x=±√p3
⇒f''(√p3)=6√(p3)>0
and f''(−√p3=−6√p3<0
Hence given cubic minima at x=√p3 and maxima at x=−√p3
Similar Questions
Ifx2−px+q=0(p,q∈Randp≠0,q≠0) has distinct real roots. Then…
View SolutionSuppose the cubic x3−px+q has three distinct real roots, where p>0 and q>0. Then which one of the following holds ?
View SolutionFunction f(x)=|px-q|+r|x|,x epsilon (-oo,oo) where pgt0,qgt0,rgt0 Will have the following value at only one point if
View Solutionमाना- त्रिघात बहुपद x3−px+q के तीन विभिन्न वास्तविक मूल है जबकि p>0 तथा q>0 है। तो निम्न में से कौन -सा एक सत्य है
View SolutionSuppose the cubic x3−px+q has three real roots where p>0 and q>0 . Then which one of the following holds ?
1) The cubic has minimum at both √p/3 and −√p/3
2) The cubic has maximum at both √p/3 and −√p/3
3)The cubic has minimum at √p/3 and maximum at −√p/3
4)The cubic has minimum at −√p/3 and maximum at √p/3
View SolutionSuppose the cubic x3−px+q has three distinct real roots, where p>0 and q>0. Then find the max and min points .
View SolutionIf 2+i√3 is a root of x3−6x2+px+q=0 (where p and q are real) then p+q is
View SolutionIf 2+i√3 is a root of x3−6x2+px+q=0 (where p and q are real) then p+q is
View Solution
