Let A={x:−1≤x≤1} = B for each of the following functions from A to B. Find whether it is surjective, injective or bijective
(i) f(x) = x2
(ii) g(x) = |x|
(iii) h(x) = x|x|
(iv) k(x)=x2
(v) l(x) = sinπx Solution in Gujrati
The correct Answer is:B, C
A={x:−1≤x≤}
B={x:−1≤x≤}
(i) f(x)=x2
Let x1,x2∈A
∴f(x1)=f(x2)⇒x12=x22
⇒x1=x2
∴ f is one-one function
Now, let y=x2⇒x=2y
⇒−1≤y≤1
⇒−2≤2y≤2⇒−2≤x≤2
Let x∈[−1,1]
∴ There are some value of y for which x does not exist. So, f not onto.
(ii) g(x) = |x|
For x=-1, g(-1) = 1
and for x = 1, g(1) = 1
∴ f is not one-one function
Let y = |x|, then y≥0
∴ f is not onto.
(iii) h(x) = x|x| = {x2x≥0−x2x<0
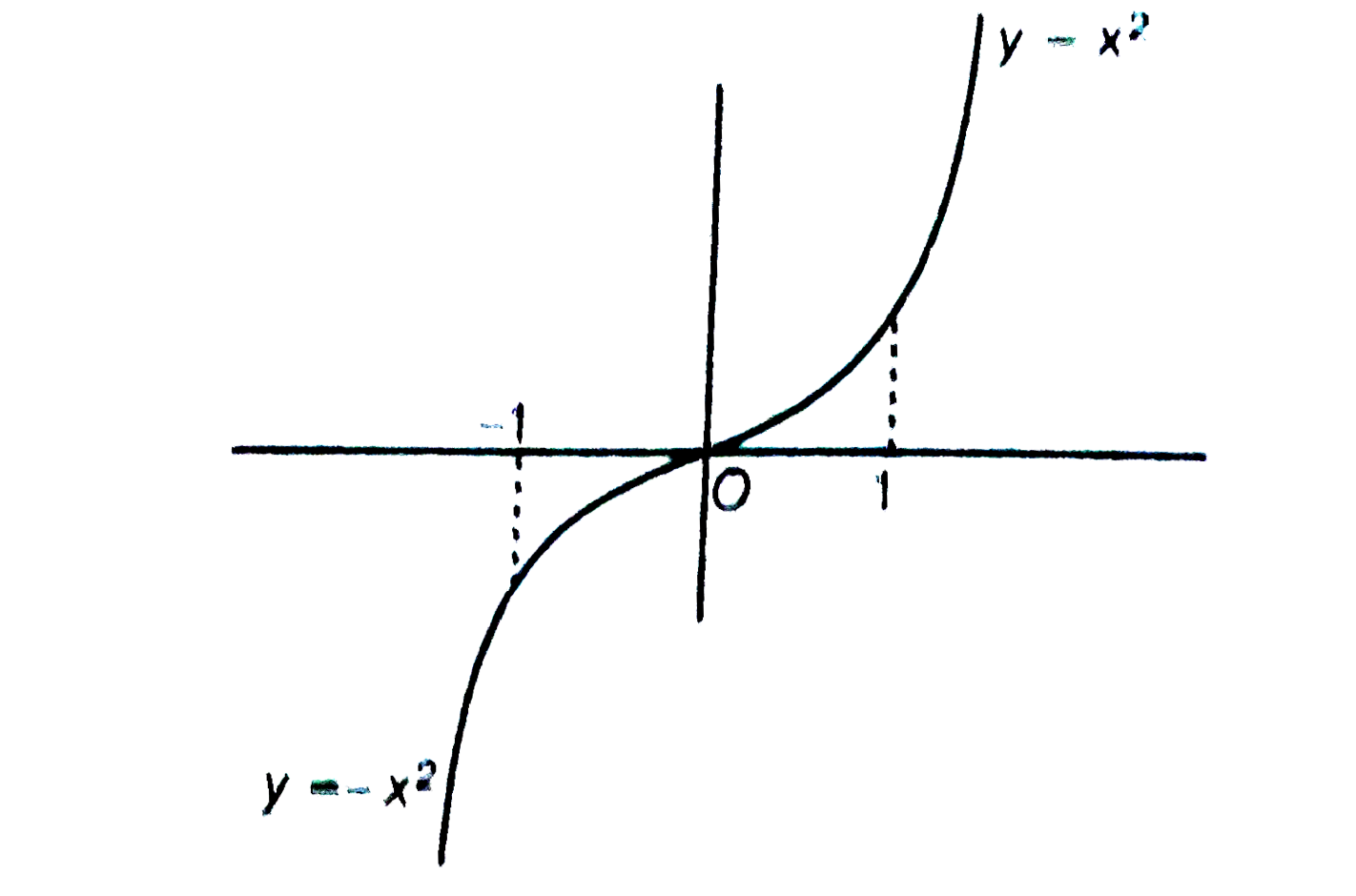
From figure, it is clear tat h is one-one and onto i.e., bijective.
(iv) k(x)=x2
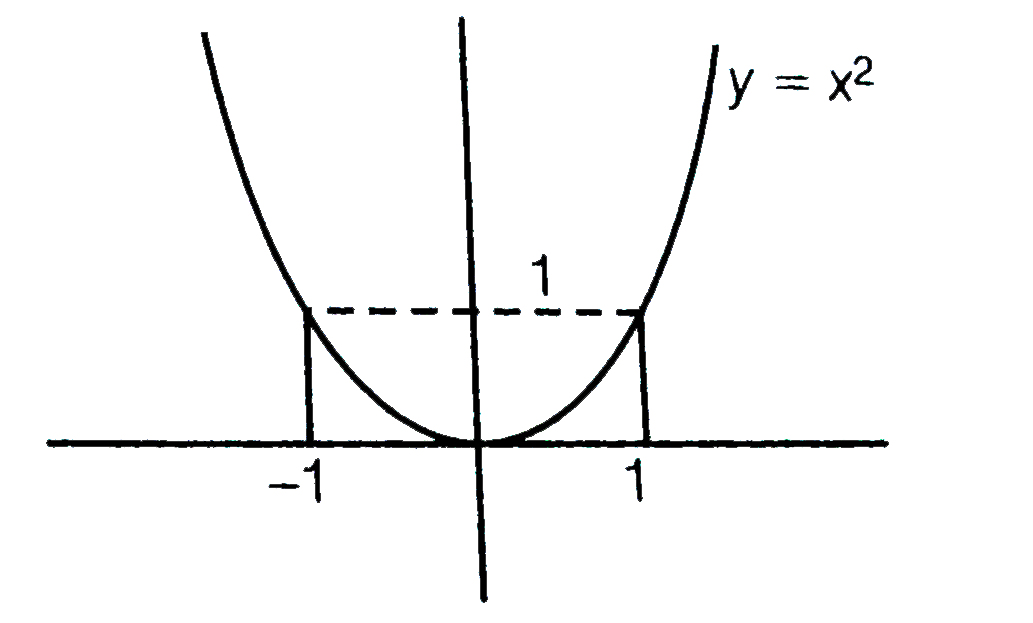
k(1) = 1
and k(-1) = 1
So, k is many-one function.
From figure, y∈(0,1)
∴ y is not onto function.
(v) y=l(x)=sinπx
for x = 1, l(1)=sinπ=0
for x = - 1, l(-1) = sin (−π) = 0
∴l is not one-one.
Now, −1≤x≤1
⇒−π≤πx≤π
⇒−1≤sinπx≤1
∴ y is onto function.
Hence, l is surjective function.
Similar Questions
Write the coefficient of x2 in each of the following br> (i)15−3x+2x2
(ii) 1−x2
(iii) πx2−3x+5
(iv)√2x2+5x−1
View SolutionLet A=[−1,1]. Then, discuss whether the following functions from A to itself are one-one onto or bijective: f(x)=x2 (ii) g(x)=|x| (iii) h(x)=x2
View SolutionLet A={x:−1≤x≤1}=B be a function f:A→B. Then find the nature of each of the following functions.
(i) f(x)=|x| (ii) f(x)=x|x|
(iii) f(x)=x3 (iv) f(x)=sinπx2
View SolutionLet A=[−1,1]. Then, discuss whether the following functions from A to itself are one-one onto or bijective: f(x)=x2 (ii) g(x)=|x| (iii) h(x)=x2
View SolutionLet A=[−1, 1] . Then, discuss whether the following functions from A to itself are one-one, onto or bijective: f(x)=x2 (ii) g(x)=|x| (iii) h(x)=x2
View SolutionLet A=[−1,1]. Then, discuss whether the following functions from A to itself are one-one onto or bijective: f(x)=x2 (ii) g(x)=|x| (iii) h(x)=x2
View SolutionLet f:N→Zandf(x)=[x−12when x is odd−x2when x is even, then:
(a). f (x) is bijective (b).f (x) is injective but not surjective (c).f (x) is not injective but surjective (d).f (x) is neither injective nor subjective
View SolutionLet A={x:-1 le x le 1}=B be a function f: A to B. Then find the nature of each of the following functions. (i) f(x) = |x| " (ii) " f(x)=x|x| (iii) f(x)=x^(3) " (iv) " f(x)="sin"(pi x)/(2)
View Solution
