An oscillation is superposition of three harmonic oscillations and decribed by the equation x=Asin2πυ1 where A changes with time according to A=A0(1+cos2πυ2t) with A0 to be constant. The frequencies of pure harmonic oscillations forming this oscillation are Solution in Gujrati
(a)υ1,υ2,υ1−υ2
(b)υ1,υ2,υ1+υ2
(c)υ1,υ1+υ2,υ1−υ2
(d)υ2,υ1+υ2,υ1−υ2
The correct Answer is:B
x=A0(1+cos2πγ2t)sin(πγ1)
=A0[sin2πγ1t+cos2πγ2t+sin2πγ1t]
=A0[sin2πγ1t+12sin(2π(γ1+γ2)t−12sin(2π(γ1−γ2t)]
Required ratio =v1:(v1−v2):(v1+v2)
टॉपर्स ने हल किए ये सवाल
- SIMPLE HARMONIC MOTIONBook:ALLEN Chapter:SIMPLE HARMONIC MOTIONExercise:Exercise-02
Explore 19 Videos
- SIMPLE HARMONIC MOTIONBook:ALLEN Chapter:SIMPLE HARMONIC MOTIONExercise:Exercise- 3 Match The Column
Explore 1 Video
- SIMPLE HARMONIC MOTIONBook:ALLEN Chapter:SIMPLE HARMONIC MOTIONExercise:SOME WORKED OUT EXAMPLES
Explore 29 Videos
- RACEBook:ALLEN Chapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
- TEST PAPERBook:ALLEN Chapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
समान प्रश्न
A mass M is performing linear simple harmonic motion. Then correct graph for acceleration a and corresponding linear velocity v is
View SolutionColumn-I gives different situtions in which bodes are floating in liquid. Column-II gives correspoding time periods of oscillation.
_E01_069_Q01.png)
A cube floating in liquid.
View SolutionA simple pendulum has time period 2s. The point of suspension is now moved upward accoding to relation y=(6t−3.75t2)m where t is in second and y is the vertical displacement in upward direction. The new time period of simple pendulum will be
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionAn oscillation is superposition of three harmonic oscillations and decribed by the equation x=A sin 2pi upsilon_(1) where A changes with time according to A=A_(0)(1+cos 2pi upsilon_(2)t) with A_0 to be constant. The frequencies of pure harmonic oscillations forming this oscillation are
View SolutionThe superposition of two harmonic oscillations of the same direction results in the oscillation of a point according to the law x=a cos 2.1 t cos 50.0 t , where t is expressed in seconds. Find the angular frequencies of the constituent oscillations and the period with which they beat.
View SolutionA mass m oscillates with simple harmonic motion with frequency f=ω2πand amlitude A on a spring with constant K. therefore
View SolutionThe velocity-time diagram of a harmonic oscillator is shown in the adjoining figure. The frequency of oscillation is
View SolutionIn forced oscillations , a particle oscillates simple harmonically with a frequency equal to
View Solution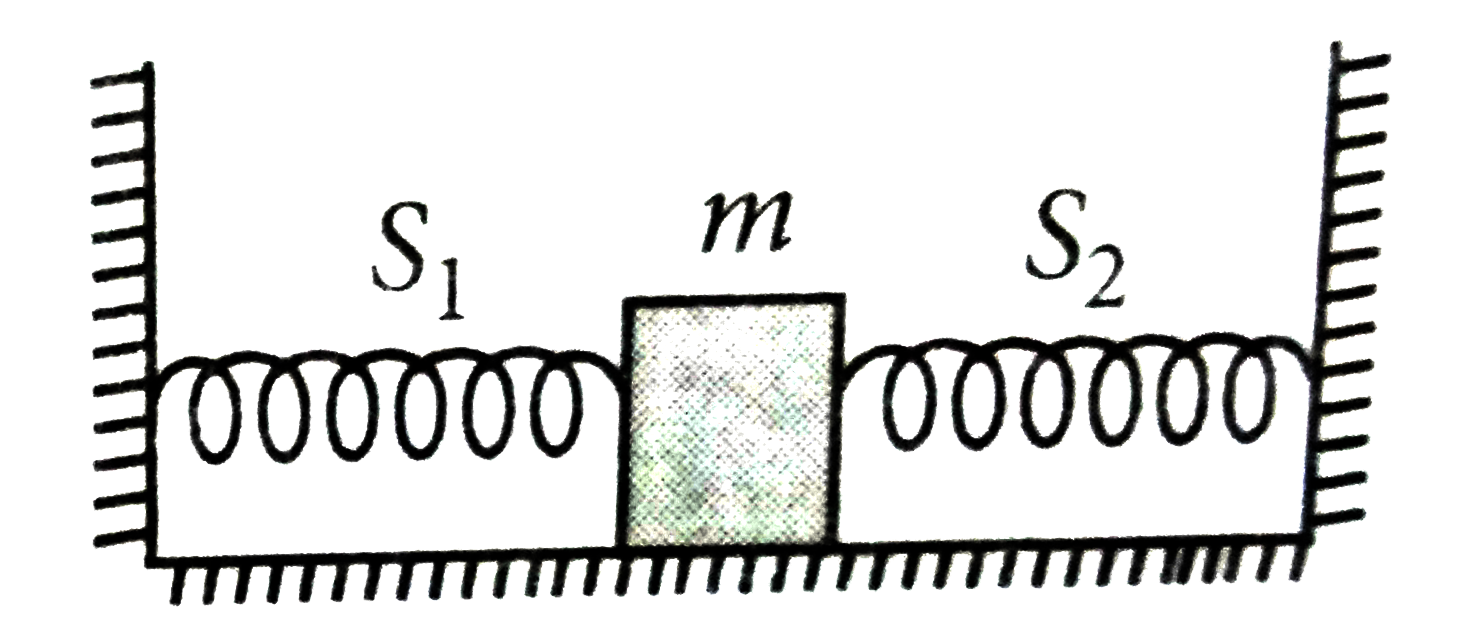
When a mass m is connected individually to two springs S1andS2, the oscillation frequencies are υ1andυ2. If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be
View SolutionWhat is meant by angular harmonic oscillations? Compute the time period of angular harmonic oscillation. Time period and frequency of angular SHM:
View SolutionThe position of a simple harmonic oscillator is given by x(t)=(0.50)cos(π3t), where t is measured in seconds. What is the maximum velocity of this oscillator?
View SolutionFor a simple harmonic oscillator the frequency of oscillation is independent of
View SolutionWhen a mass m is connected individually to two springs S_(1) and S_2 , the oscillation frequencies are upsilon_(1) and upsilon_(2) . If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be
View SolutionFor a simple harmonic oscillator the frequency of oscillation is independent of
View Solution
