In y=Asinωt+Asin(ωt+2π3)
∣∣
∣
∣
∣
∣
∣
∣
∣
∣∣Column-IColumn-II(A)Motion(p)is periodic but no SHM(B)Amplitude(q)is SHM(C)Initial phase(r)A(D)Maximum velocity(s)π/3(t)ωA/2(u)None∣∣
∣
∣
∣
∣
∣
∣
∣
∣∣ Solution in Gujrati
The correct Answer is:A, B, C, D
y=Asinωt+Asinωtcos'2π3+Acosωtsin'2π3
=A2sinωt+A√32cosωt=Asin(ωt+π3)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Asseration & Reason
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (1)
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column
1 Video
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
Statement-1 : The motion of simple pedulum is simple harmonic only for a <<l.
Statement-2 : Motion of a simple pendulum is SHM for small angular displacement.
_E01_073_Q01.png)
View SolutionPassage IV) Angular frequency in SHM is given by ω=√km. Maximum acceleration in SHM is ω2 A and maximum value of friction between two bodies in contact is μN, where N is the normal reaction between the bodies.
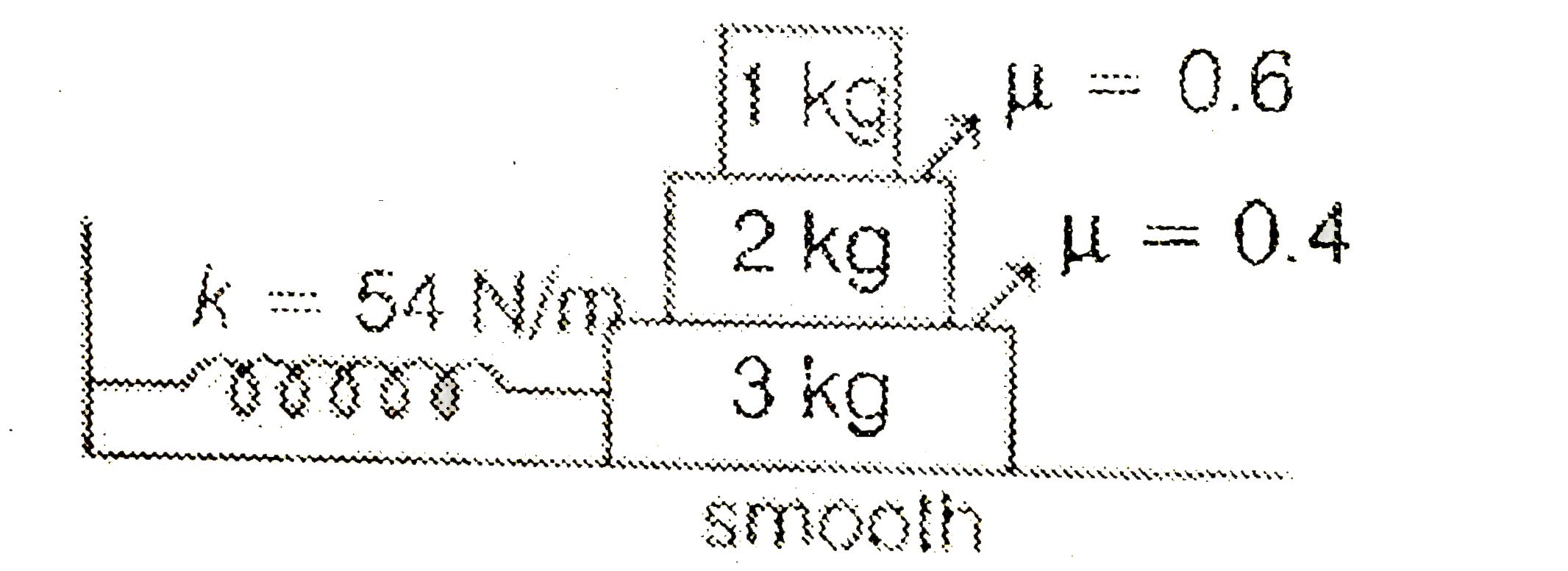
In the figure shown, what can be the maximum amplitude of the system so that there is no slipping between any of hte blocks?
View SolutionColumn-I gives different situtions in which bodes are floating in liquid. Column-II gives correspoding time periods of oscillation.
_E01_069_Q01.png)
A cube floating in liquid.
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionThe initial position and velocity of a body moving in SHM with period T=0.25s are x=5.0cm and v=218cm/s. What are the amplitude and phase constant of the motion ?
View SolutionA particle is subjected to SHM as given by equation x_1=Asinomegat and x_2=A_2sin(omegat+(pi)/(3)) . The maximum acceleration and amplitude of the resultant motion are a_(max) and A , respectively Then.
View SolutionSound is travelling in a long tube towards right and the graph of excess pressure variation Vs position (at some instant) is given below.
 Match velocities in column-I with column-II P,Q,R,S,T are medium particles inside the tube.
Match velocities in column-I with column-II P,Q,R,S,T are medium particles inside the tube.
Column-IColumn-II(A)velocity is towards right(P)P(B)velocity is towards left(Q)Q(C)velocity is zero(R)R(D)Speed is maximum(S)S(T)T
View SolutionThe acceleration- time graph of a particle executing SHM along x-axis is shown in figure. Match Column-I with column-II

Column-IColumn-IIPosition of particlePhysical,quantites related with particle's motion(A)At position 1 (p)Kinetic energy is maximum(B)At position 2 qPotential energy is maximum(C)At position 3(r)Displacement of particle is negative(D)At position 4(s)Velocity is maximum
View SolutionMatch Column - I with Column - II
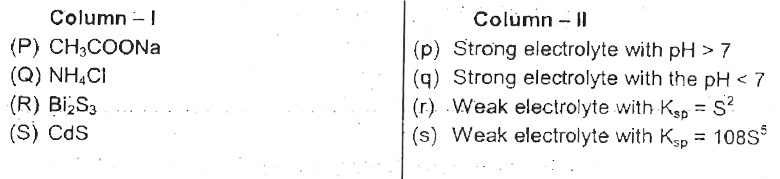
PQRS(A)1243(B)2143(C)4132(D)4321
View SolutionAmplitude of a SHM is, A = 7 cm, its time period, T = 2s and initial phase, alpha=30^(@) . Establish the equation of this SHM.
View SolutionFind the maximum velocity of a SHM particle having amplitude 'A' and periodic time T.
View SolutionMatch Column A with Column B

(A) (P-i), (Q-ii), (R-iv), (S-iii)
(B) (P-ii), (Q-i), (R-iii), (S-iv)
(C) (P-ii), (Q-iii), (R-iv), (S-i)
(D) (P-iv), (Q-iii), (R-ii), (S-i)
View SolutionMatch the following
Column-I Column-IIA) Linear combination of two SHMsP) T=√Rg (R is radius of the earth) B) y=Asinω1t+Asin(ω2t+ϕ)Q) SHM for equal frequencies and amplitude C) Time period of a pendulum of infinite length R) Super position may not always be an SHM D) Maximum value of time period an oscillating pendulumS) Amplitude will be √2Afor ω1=ω2 and phase difference of π2
View SolutionColumn-IColumn-IIA) Motion of needle of sewing machine P) Periodic oscillatory B) Motion of conical pendulum Q) Oscillatory non-eriodic C) Motion of simple pendulum R) Oscillatory, linear simple harmonic D) Motion of suspended loaded spring S) Oscillatory, Non linear SHM pulled and released
View SolutionIn column-l, the projection of a particle moving along a circle (uniformly) in x-y plane with its centre of origin along x and y axes, while in Column-II, the description of particle's motion is given. It is given that particle's angular velocity is constant and equal to ω and the radius of circle is A,δ≠0,π2orπ For this situation match the column-I with column-II
Column - IColumn - IIA) x(t)=Asin(ωt+δ−π2),y(t)=Asin(ωt+δ)P) Uniform circular motion (clockwise)B) x(t)=Asin(ωt+δ),y(t)=Asin(ωt+δ+π2)Q) Uniform circular motion(anti - clockwise)C) x(t)=Asin(ωt),x(t)=Acos(ωt)R) At = 0 particle is neither on x - axis nor on y - axisD) x(t)=Acos(ωt+δ),y(t)=Acos(ωt+δ+π2)S) At t = 0 particle is either on x - axis on y - axis
View Solution

