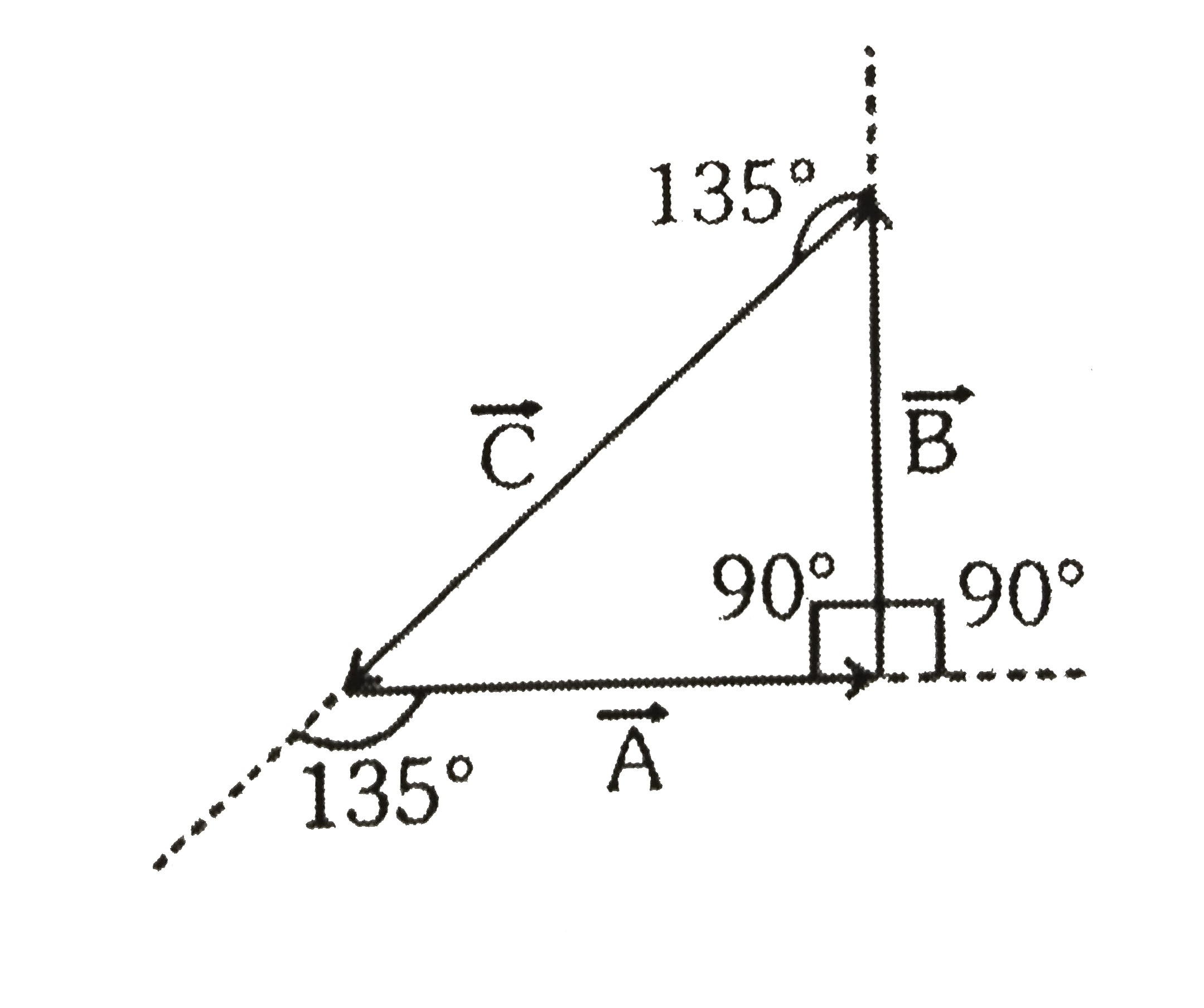
Given that →A+→B+→C=→0. Out of these three vectors two are equal in magnitude and the magnitude of the third vector is √2 times as that of either of the two having equal magnitude. Then the angles between vectors are given by : Solution in Gujrati
30∘,60∘,90∘
45∘,45∘,90∘
45∘,60∘,90∘
90∘,135∘,135∘
The correct Answer is:4
→A+→B+→C=→0
A=B=a,andC=√2a
Topper's Solved these Questions
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-II AIPMT/NEET & AIIMS (2006- 2018)
6 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
Similar Questions
Assertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionThe vector →A and →B are such that ∣∣→A+→B∣∣=∣∣→A−→B∣∣. The angle between vectors →A and →B is -
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View Solutiongiven that →A+→B+→C=0 out of three vectors two are equal in magnitude and the magnitude of third vector is √2 times that of either of the two having equal magnitude. Then the angles between vectors are given by
View SolutionGiven that →A+→B+→C=0, out of three vectors two are equal in magnitude and the magnitude of third vector is √2 times that of either of two having equal magnitude. Then angle between vectors are given by
View Solutionif →a,→band→c are mutally perpendicular vectors of equal magnitudes, then find the angle between vectors and →a+→b+→c.
View SolutionTwo vectors →A and →B have equal magnitudes. If magnitude of →A+→B is equal to n times the magnitude of →A−→B, then the angle between →A and →B is :-
View Solutionयदि →a,→b,→c बराबर परिमाण के परस्पर लम्ब सदिश हो तो दिखाइए कि सदिश →a+→b+→c सदिशों →a,→b,→c से बराबर कोण बनाता है।
View SolutionThe resultant of two vectors of equal magnitude is equal to the magnitude of either of the two vectors. What is the angle between the two vectors ?
View SolutionGiven : vec(a) + vec(b) + vec(c) = 0 . Out of the three vectors vec(a), vec(b) and vec(c) , two are equal in magnitude. The magnitude of the third vector is sqrt(2) times that of either of the two having equal magnitude. The angles between the vectors are :
View SolutionThe resultant of two vectors →A and →b is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. The angle between →A and →B is
View Solutionदिया है →A+→B+→C=0 तीन में से दो सदिश परिमाण में समान हैं तथा तीसरे सदिश का परिमाण पहले दो समान परिमाण वाले सदिशों में से किसी एक का √2 गुना है तो सदिशों के मध्य कोण है
View SolutionGiven that →A+→B+→C=0 out of three vectors two are equal in magnitude and the magnitude of third vector is √2 times that of either of two having equal magnitude. Then angle between vectors are given by
View Solutionदिया है →A+→B+→C=→0 इन तीन सदिशों में से दो सदिशों के परिमाण समान है तो तीसरे सदिश का परिमाण, समान परिमाण वाले किसी एक सदिश के परिमाण का √2 गुना है । तो सदिशों के मध्य कोण होंगें (क्रमशः)
View Solutionif →a,→band→c are mutally perpendicular vectors of equal magnitudes, then find the angle between vectors and →a+→b+→c.
View SolutionGiven that vecA+vecB+vecC=0 , out of three vectors two are equal in magnitude and the magnitude of third vector is sqrt2 times that of either of two having equal magnitude. Then angle between vectors are given by
View Solution

