Electric field at centre of a uniforly charged semicirlce of radius a is
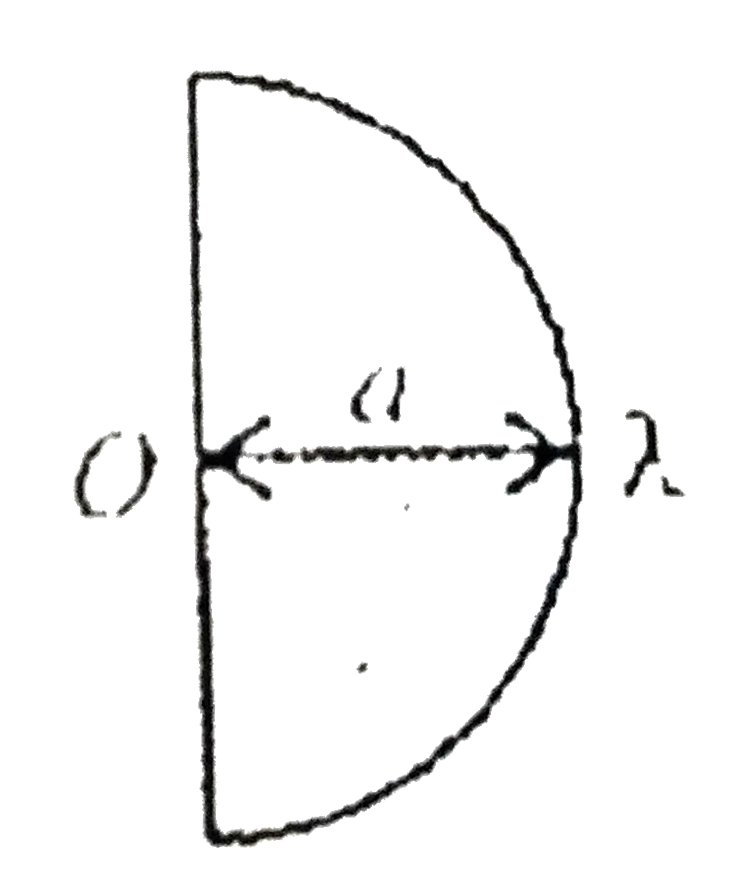
λ2πε0a3
λ2πε0a2
λ22πε0a
λ2πε0a
The correct Answer is:D
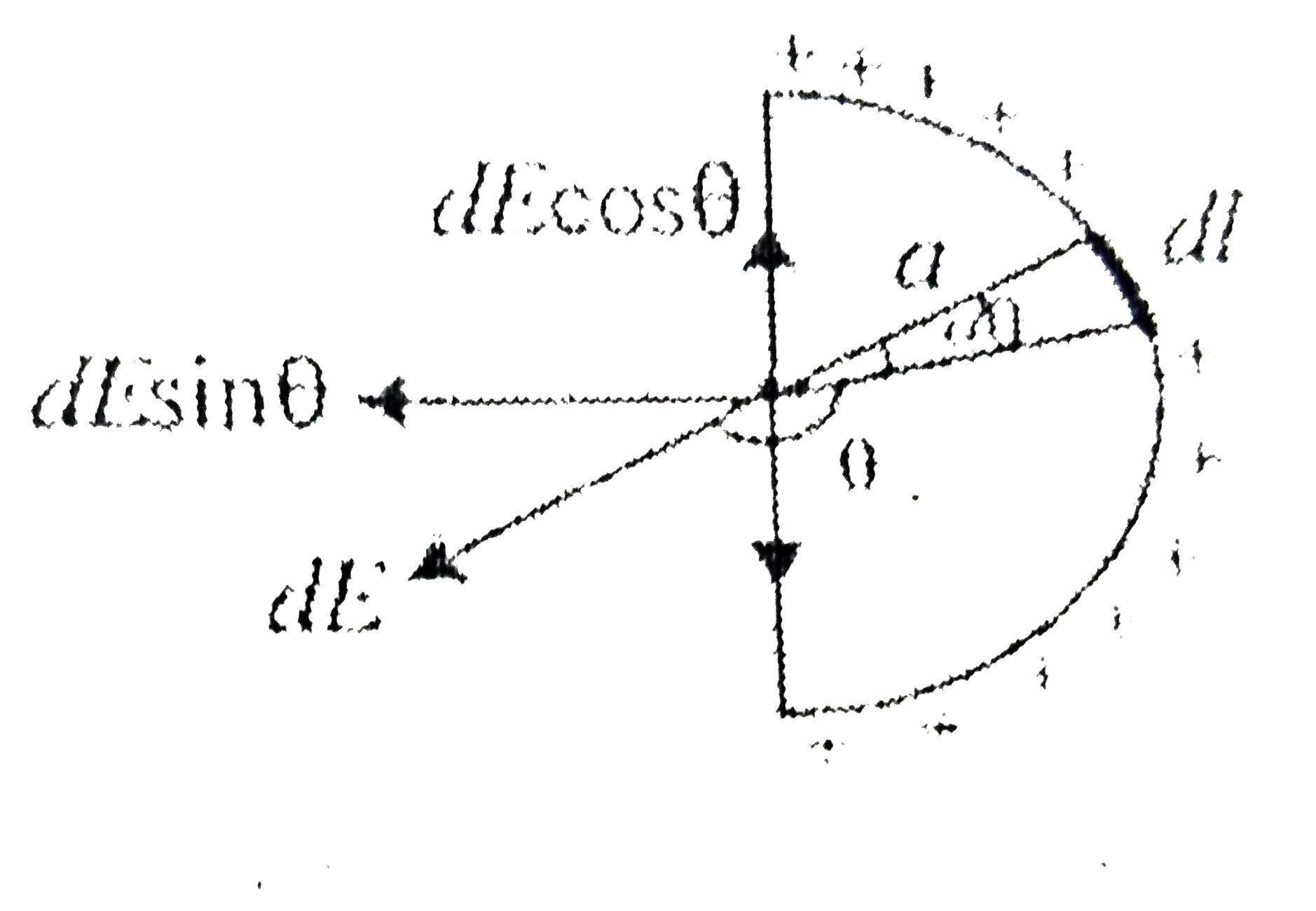
Electtric field intensity at O due to small elemental length dl of charged ring .
dE=14πε0⋅λdla2=14πε0⋅λadθa2
dE=14πε0⋅λadθ
∴ Net electric field at centre O is
E = ∫dEsinθ=π∫014πε0λasinθdθ
=λ4πε0a[−cosθ]π0
∴E=λ2πε0a.
Similar Questions
A conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
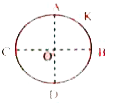
View SolutionA thin conducting ring of radius R is given a charge +Q. The electric field at the centre o of the ring due to the charge on the part AKB of the ring is E. The electric field at the centre due to the charge on the part ACDB of the ring is
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is lamda
View SolutionA conducting sphere of radius R is given a charge Q . The electric potential and the electric field at the centre of the sphere respectively are
View SolutionThe electric field stength due to a circular loop of charge of radius R and linear density of charge λ at its centre is proportional to:
View SolutionA conducting sphere of radius R is given a charge Q . The electric potential and the electric field at the centre of the sphere respectively are
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View Solution
