Solve |x−1|+|x−2|≥4Solution in Bengali
Video Solution
Text Solution
Let f(x)=|x−1|+|x−2|
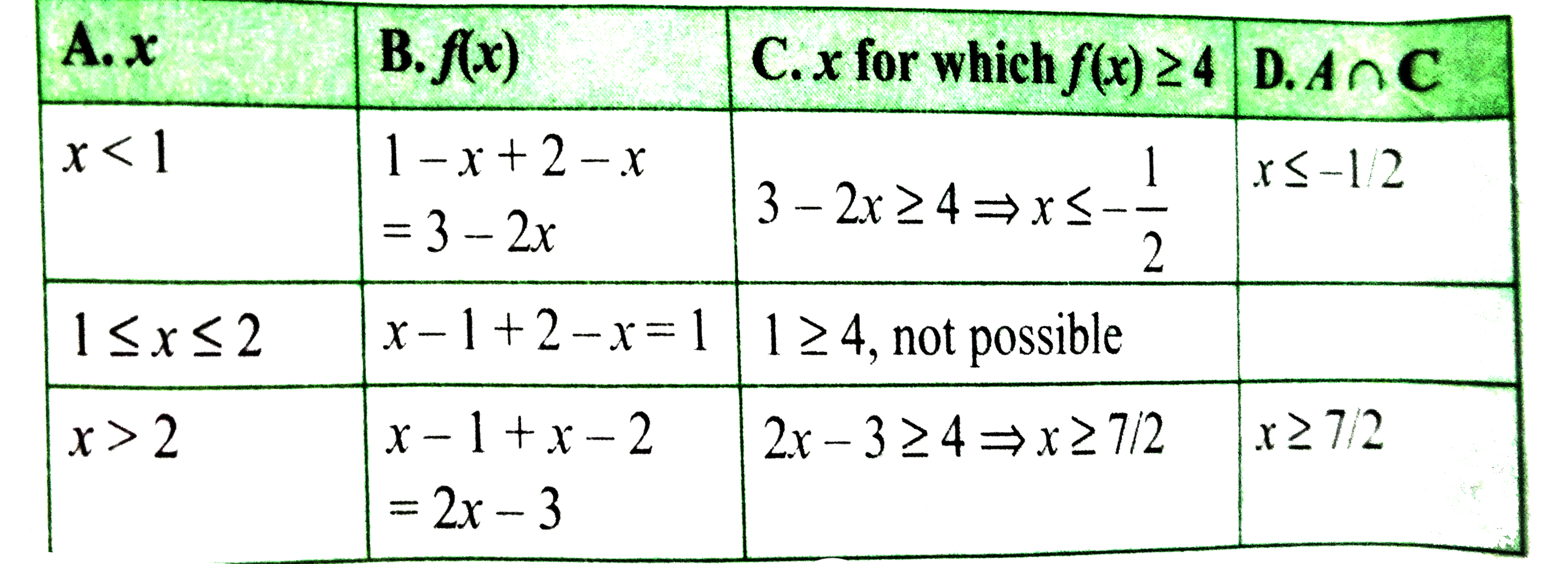
Hence, solutions is x∈(−∞,−1/2]∪[7/2,∞).
Alternative Method:
Consider |x−1|+|x−2|<4
Now, |(x−1)+(x−2)|≤|x−1|+|x−2|
∴|(x−1)|+(x−2)∣<4
⇒|2x−3|<4
⇒−4<2x−3<4
⇒−1<2x<7
⇒−1/2<x<7/2
Therefore, for |x−1|+|x−2|≥4, we have
x∈(−∞,−1/2]∪[7/2,∞).
|
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
View SolutionIf A,B and C are three sets such that A∩B=A∩CandA∪B=A∪C then
View Solutionsolve: |x−2|+|x−4|≥8
View Solutionsolve : 3x−42+1≥x+14
View SolutionSolve : |x−1|+|x−2|≥3
View SolutionSolve |x−1|+|x−2|≥4
View SolutionSolve : |x|−|x−2|≥1
View Solutionहल कीजिए 3x−42+1≥x+14
View Solutionहल कीजिए |x−1|+|x−2|≥3
View Solutionहल कीजिए
|x−1|+|x−2|≥4
View SolutionSolve the inequality 3x−42≥x+14−1.
View SolutionSolve |x−1|+|x−2|≥4
View SolutionSolve |x−1|+|x−2|≥4
View SolutionSolve |x−1|+|x−2|≥4
View SolutionSolve : |x|−|x−2|≥1
View Solutionsolve: |x−2|+|x−4|≥8
View Solution

