Consider two curves C1:y=1xandC2:y=logx on the xy plane. Let D1 denotes the region surrounded by C1,C2, and the line x=1andD2 denotes the region surrounded by C1,C2 and the line x=a. If D1=D2, then the sum of logarithm of possible value of a is _____________Solution in Bengali
The correct Answer is:1
Given that D1=D2
c∫1(1x−logx)dx=a∫c(logx−1x)dx
(−1x2−x(logx−1))c1=(x(logx−1)+1x2)ac
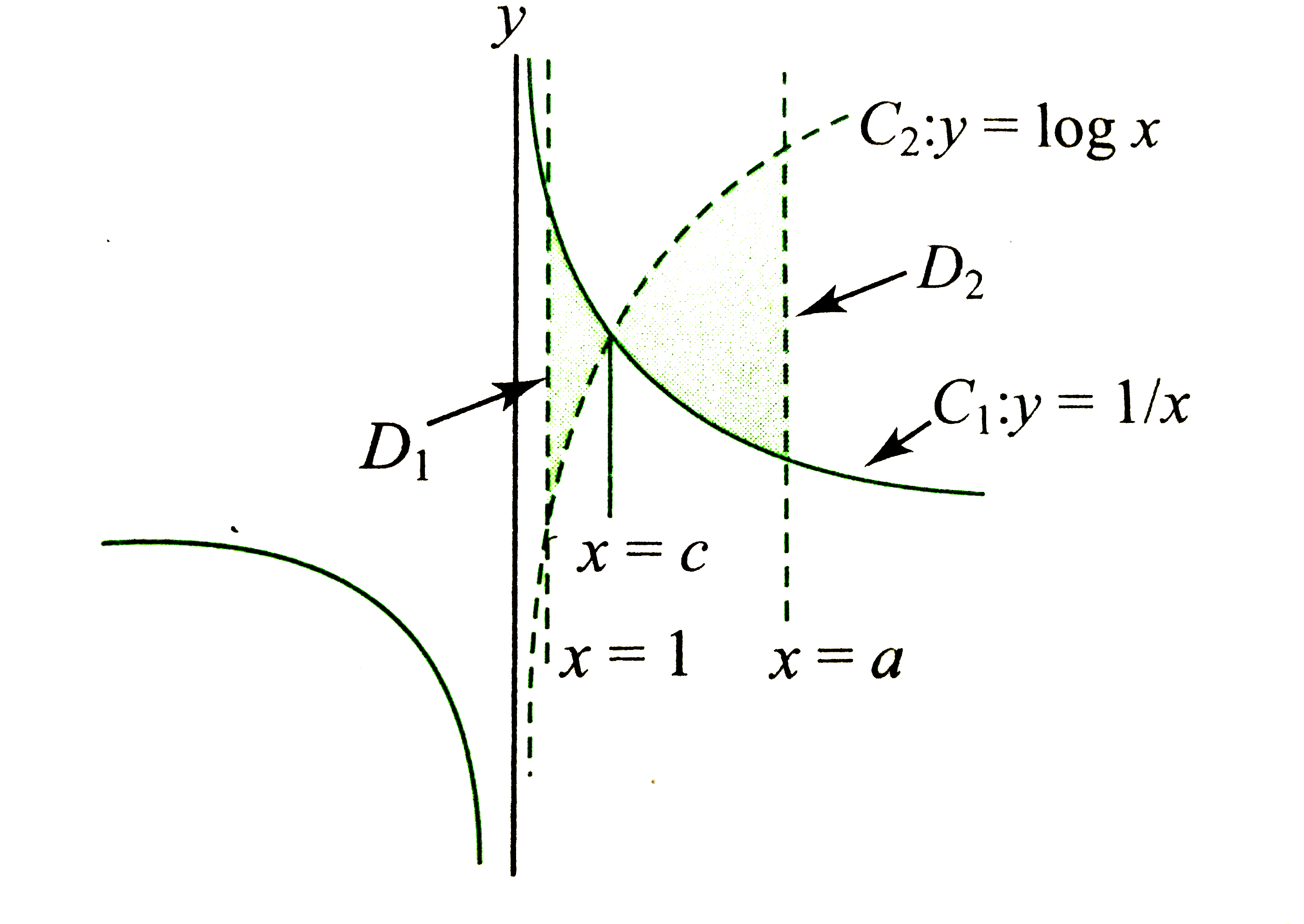
∴ 0=a(loga−1)+1a2
∴ a=1
Topper's Solved these Questions
- AREABook:CENGAGE PUBLICATIONChapter:AREAExercise:Archives
Explore 10 Videos
- AREABook:CENGAGE PUBLICATIONChapter:AREAExercise:Single Correct Answer Type
Explore 30 Videos
- AREABook:CENGAGE PUBLICATIONChapter:AREAExercise:Matrix Match Type
Explore 4 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGE PUBLICATIONChapter:APPLICATIONS OF DERIVATIVESExercise:Comprehension Type
Explore 3 Videos
- BINOMIAL THEOREMBook:CENGAGE PUBLICATIONChapter:BINOMIAL THEOREMExercise:Comprehension
Explore 11 Videos
Similar Questions
The area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate x=3, and the x−aξs is 7sq.unites (b) 6sq.unites 9sq.unites (d) None of these
View SolutionLet the straight line x= b divide the area enclosed by y=(1−x)2,y=0,andx=0 into two parts R1(0≤x≤b)andR2(b≤x≤1) such that R1−R2=14. Then b equals
View SolutionMatch the following lists :

View SolutionLet f(x) be a function such that its derovative f'(x) is continuous in [a, b] and differentiable in (a, b). Consider a function ϕ(x)=f(b)−f(x)−(b−x)f'(x)−(b−x)2A. If Rolle's theorem is applicable to ϕ(x) on, [a,b], answer following questions.
If there exists some unmber c(a lt c lt b) such that ϕ'(c)=0andf(b)=f(a)+(b−a)f'(a)+λ(b−a)2f''(c), then λ is
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIIf y=1+c_1/(x-c_1)+(c_2x)/((x-c_1)(x-c_2))+(c_3 x^2)/((x-c_1)(x-c_2)(x-c_3)) show that dy/dx=(y/x)[c_1/(c_1-x)+c_2/(c_2-x)+c_3/(c_3-x)]
View SolutionLet 'a' be a positive constant number. Consider two curves C_1: y=e^x, C_2:y=e^(a-x). Let S be the area of the part surrounding by C_1, C_2 and the y axis, then Lim_(a->0) s/a^2 equals (A) 4 (B) 1/2 (C) 0 (D) 1/4
View SolutionIf the lines whose equations are y=m1x+c1,y=m2x+c2andy=m3x+c3 meet in a point, then prove that : m1(c2−c3)+m2(c3−c1)+m3(c1−c2)=0
View SolutionIf (1+x)n=C0+C1x+C2x2+….....+Cnxn, then C0+2.C1+3.C2+….+(n+1).Cn=
View SolutionConsider the curves C1:y2andC2:x2+y2−6x+1=0
Assertion (A) The common tangents to the curves C1andC2 are othogonal.
Reason ( R ) x-y+1=0 and x+y+1=0 are the common tangents to the curves C1andC2 The correct answer is
View SolutionConsider two curves C1:y=1xandC2:y=1nx on the xy plane. Let D1 denotes the region surrounded by C1,C2, and the line x=1andD2 denotes the region surrounded by C1,C2 and the line x=a. If D1=D2, then the sum of logarithm of possible value of a is _____________
View SolutionTwo circles C1 and C2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB and QY meets circles C1 andC2 at Xa n dZ respectively. Then prove that Y is the midpoint of XZ
View SolutionThe value of ∣∣111nCn+21Cn+41Cn1Cn+22Cn+42C2∣∣ is
View SolutionShow that the area of the triangle formed by the lines y=m1x+c1,y=m2x+c2 and x=0 is (c1−c2)22|m1−m2|
View SolutionC1:y=1x और C2:y=Inx, xy समतल में दो वक्र है। माना D1 वह क्षेत्र है जो कि C1,C2, और रेखा x= 1 से परिबद्ध है और D2 वक्रों C1,C2, और रेखा x= a से परिबद्ध क्षेत्र है। यदि D1=D2 हो, तब a का मान ज्ञात कीजिये।
View SolutionLet 'a' be a positive constant number. Consider two curves C1:y=ex,C2:y=ea−x. Let S be the area of the part surrounding by C1,C2 and the y axis, then Lima→0sa2 equals (A) 4 (B) 12 (C) 0 (D) 14
View Solution
