Let A,B,C be angles of triangles with vertex A≡(4,−1) and internal angular bisectors of angles B and C be x−1=0 and x−y−1=0 respectively.
Slope of BC is Solution in Bengali
1/2
2
3
12
The correct Answer is:B
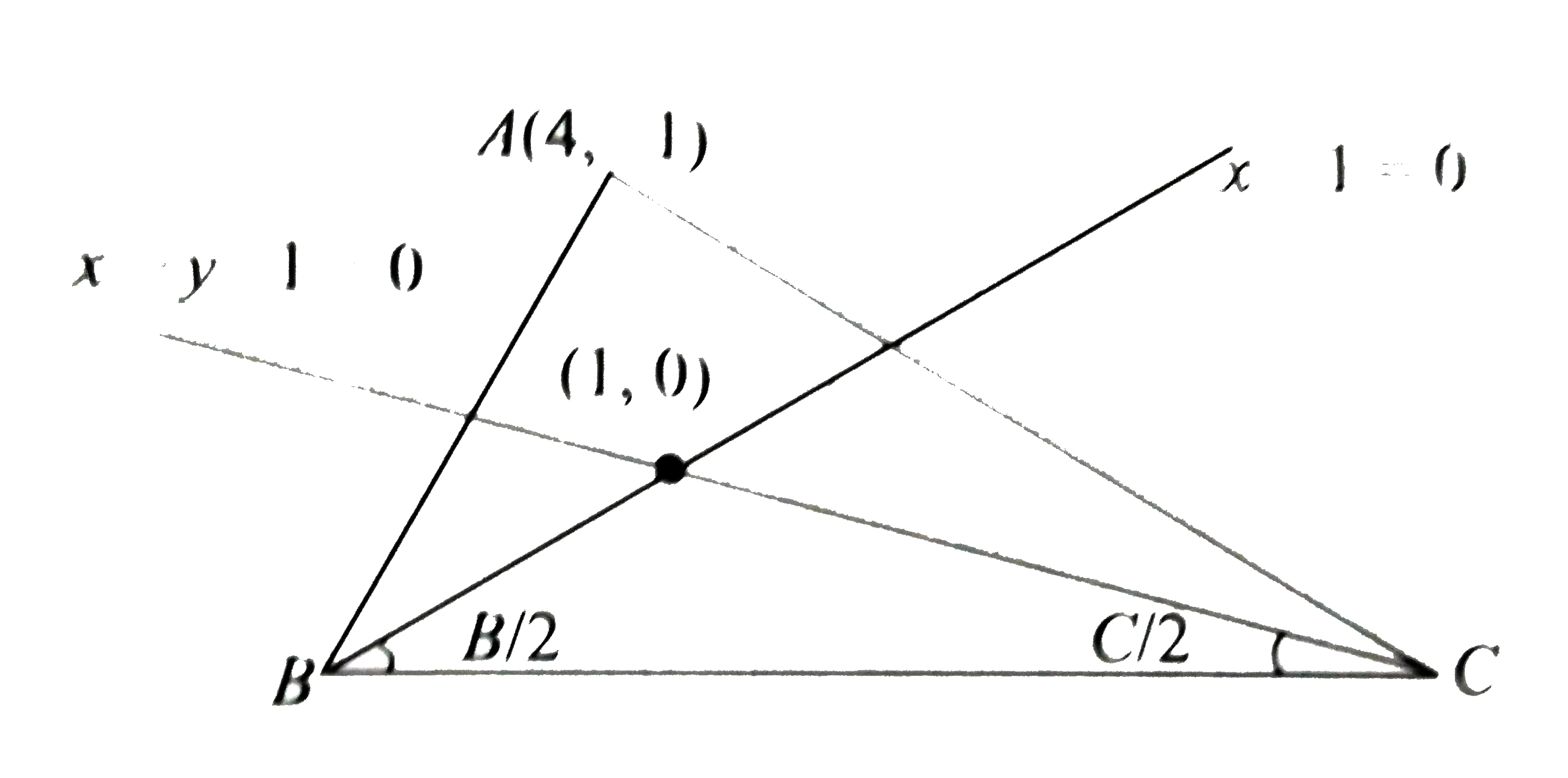
Image of A(4,−1) in bisectors of B and C lies on side BC
⇒ Image of A(4,−1) with respect to x−y−1=0 is
x−41=y+1−1=−2(4+1−1)2⇒(0,3)
Image of A(4,−1) with respect to x−1=0 is
x−41=y+10=−2(4−1)1⇒(−2,−1)
Hence, slope of BC is m=(3+10+2)=2
टॉपर्स ने हल किए ये सवाल
- STRAIGHT LINEBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- STRAIGHT LINEBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- STATISTICSBook:CENGAGE PUBLICATIONChapter:STATISTICSExercise:Archives
Explore 10 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:ARCHIVES (NUMERICAL VALUE TYPE)
Explore 1 Video
समान प्रश्न
The point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionIf the mean deviation of the numbers 1,1+d,1+2d,...,1+100d from their mean is 255, then the d is equal to
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionLet ABC be a triangle. Let A be the point (1,2),y=x be the perpendicular bisector of AB, and x−2y+1=0 be the angle bisector of ∠C . If the equation of BC is given by ax+by−5=0 , then the value of a+b is (a)1(b) 2(c) 3 (d) 4
View SolutionLet ABC be a triangle such that the coordinates of the vertex A are (3,1). Equation of the median through B is 2x+y-3=0 and equation of the angular bisector of C is 7x-4y-1=0. Find the slope of line BC.
View SolutionLet A,B,C be angles of triangles with vertex A≡(4,−1) and internal angular bisectors of angles B and C be x−1=0 and x−y−1=0 respectively.
Slope of BC is
View SolutionLet A,B,C be angles of triangles with vertex A≡(4,−1) and internal angular bisectors of angles B and C be x−1=0 and x−y−1=0 respectively.
If A,B,C are angles of triangle at vertices A,B,C respectively then cot(B2)cot.(C2)=
View SolutionIn △ABC, the coordinates of the vertex A are , (4,−1) and lines x−y−1=0and2x−y=3 are the internal bisectors of angles B and C . Then the radius of the circles of triangle AbC is
View SolutionThe vertices of a triangle are A(0, 0), B(1, 0) and C(0, 2). The point of intersection of bisectors of internal angles is
View SolutionLet in ΔABC the coordinates of A are (0, 0). Internal angle bisector of ∠ABC is x−y+1=0 and mid - point of BC is (−1,3). Then, the ordinate of C is
View SolutionIn △ABC, the coordinates of the vertex A are , (4,−1) and lines x−y−1=0and2x−y=3 are the internal bisectors of angles B and C . Then the radius of the circles of triangle AbC is
View SolutionLet ABC be a triangle. Let A be the point (1,2),y=x be the perpendicular bisector of AB, and x−2y+1=0 be the angle bisector of ∠C . If the equation of BC is given by ax+by−5=0 , then the value of a+b is (a)1(b) 2(c) 3 (d) 4
View SolutionIn △ABC, vertex A is (1, 2). If the internal angle bisector of ∠B is 2x−y+10=0 and the perpendicular bisector of AC is y = x, then find the equation of BC
View SolutionLet A,B,C be angles of triangles with vertex A≡(4,−1) and internal angular bisectors of angles B and C be x−1=0 and x−y−1=0 respectively.
Slope of BC is
View SolutionLet A,B,C be angles of triangles with vertex A≡(4,−1) and internal angular bisectors of angles B and C be x−1=0 and x−y−1=0 respectively.
If A,B,C are angles of triangle at vertices A,B,C respectively then cot(B2)cot.(C2)=
View Solution
