If the inequality cot2x+(k+1)cotx−(k−3)<0 is true for at least one x∈(0,π/2), then k∈.
(−∞,3−2√5)
(3,∞)
(−1,∞)
(−∞,3)
The correct Answer is:1,2
Let cot x = t.
Since x∈(0,π/2),t∈(0,∞)
Therefore, f(t)=t2+(k+1)t−(k−3)<0 for at least one t∈(0,∞) .
We have following possibilities for the graph of f(t).
Case I :
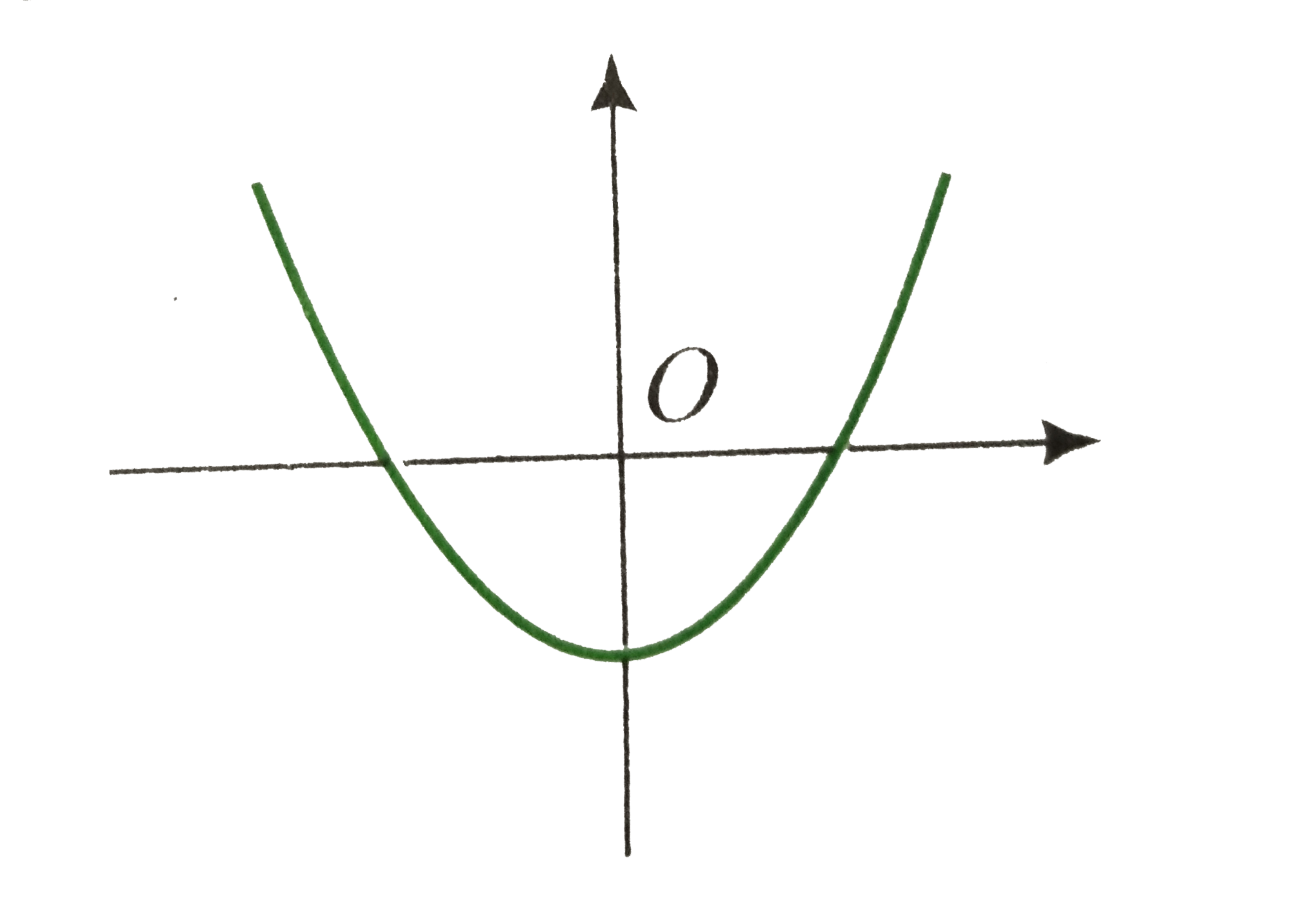
f(0)<0⇒k>3
Case II :

D>0
⇒(k+1)2+4(k−3)>0
⇒k2+6k−11>0
⇒(k+3)2>20
⇒k+3<−2√5ork+3>2√5
⇒k<−3−2−√2ork>−3+2√5
−b2a>0
⇒−(k+1)>0
⇒k<−1.....(2)
⇒k(0)≥0
⇒−k+3≥0
⇒k≤3....(3)
From (1),(2) and (3) we get
k∈(−∞,−3−2√5)
So, from the both cases, k∈(−∞,−3−2√5)∪(3,∞)
Topper's Solved these Questions
- THEORY OF EQUATIONSBook:CENGAGE PUBLICATIONChapter:THEORY OF EQUATIONSExercise:Linked Comprechension Type
Explore 37 Videos
- THEORY OF EQUATIONSBook:CENGAGE PUBLICATIONChapter:THEORY OF EQUATIONSExercise:MATRIX MATCH TYPE
Explore 6 Videos
- THEORY OF EQUATIONSBook:CENGAGE PUBLICATIONChapter:THEORY OF EQUATIONSExercise:Single Correct Answer Type : Exercise
Explore 89 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:ARCHIVES (NUMERICAL VALUE TYPE)
Explore 1 Video
- THREE DIMENSIONAL GEOMETRYBook:CENGAGE PUBLICATIONChapter:THREE DIMENSIONAL GEOMETRYExercise:All Questions
Explore 291 Videos
Similar Questions
Consider an unknow polynomial which divided by (x−3) and (x−4) leaves remainder 2 and 1, respectively. Let R(x) be the remainder when this polynomial is divided by (x−3)(x−4).
If equations R(x)=x2+ax+1 has two distint real roots, then exhaustive values of a are.
View SolutionMatch the following for the equation x2+a|x|+1=0 where, a is a parameter.

View SolutionThe value of expression x4−8x3+18x2−8x+2 when x=2+√3
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
View SolutionFor what values of k is the inequality x^(2)-(k-3)x-k+6>0 valid for all real x?
View SolutionProve the following inequalities 1+cotx ≤cotx2 ∀ x∈(0,π)
View SolutionLet k be sum of all x in the interval [0,2π] such that 3cot2x+8cotx+3=0, then the value of k/π is ___________.
View SolutionIf the inequality cot2x+(k+1)cotx−(k−3)<0 is true for at least one x∈(0,π/2), then k∈.
View SolutionIf f(x)=log(sec2x)cot2x for x≠0 and k for x=0 is continuous at x=0, then k is
View SolutionIf ∫10cot−1(1−x−x2)dx=k∫10tan−1xdx, then k=
View SolutionIf f(x) is continuous at x=0, where f(x)={(sec2x)cot2x, for x≠0k, for x=0, then k=
View SolutionIf f(x)=(sec2x)cot2x,x≠0=k,x=0
is continuous at x = 0 , then k is equal to
View SolutionIf f(x)=(log)(sec2x)cot2x,forx≠0=k,forx=0
is continuous at x = 0 then k is
View SolutionLet k be sum of all x in the interval [0,2π] such that 3cot2x+8cotx+3=0, then the value of k/π is ___________.
View SolutionIf the inequality cot2x+(k+1)cotx−(k−3)<0 is true for at least one x∈(0,π/2), then k∈.
View Solution

