The angles of elevation of the top of a tower h metre tall from two different points ont he same horizontal line are x and y (x>y) . What is the distance between the points
h (tan x - tan y)
htanxtany
h(tanx−tany)tanxtany
h(tanxtany)tanx−tany
The correct Answer is:C
To find the distance between the two points from which the angles of elevation to the top of a tower are measured, we can follow these steps:
1. Understand the Problem:
We have a tower of height h meters. From two points A and B on the same horizontal line, the angles of elevation to the top of the tower are x and y respectively, where x>y.
2. Draw the Diagram:
Draw a vertical line representing the tower, label the top of the tower as point C and the bottom as point D. Mark points A and B on the horizontal line. The angle of elevation from point A to point C is x and from point B to point C is y.
3. Set Up the Right Triangles:
In triangle ABC (where A is the point on the ground, B is directly below the tower, and C is the top of the tower):
- From point A:
\tan(x) = \frac{h}{d_A} \quad \text{(where d_A isthedistancefrom A to the base of the tower)}
Thus,
dA=htan(x)
- In triangle BCD:
- From point B:
\tan(y) = \frac{h}{d_B} \quad \text{(where d_B isthedistancefrom B to the base of the tower)}
Thus,
dB=htan(y)
4. Express the Distance Between Points:
The distance d between points A and B can be expressed as:
d=dA−dB
5. Substitute the Values:
Substitute the expressions for dA and dB:
d=htan(x)−htan(y)
6. Combine the Fractions:
To combine the fractions, find a common denominator:
d=h(1tan(x)−1tan(y))=h(tan(y)−tan(x)tan(x)tan(y))
Since x>y, tan(x)>tan(y), thus:
d=h⋅tan(x)−tan(y)tan(x)tan(y)
7. Final Result:
Therefore, the distance d between the two points is given by:
d=h⋅tan(x)−tan(y)tan(x)tan(y)
We have a tower of height h meters. From two points A and B on the same horizontal line, the angles of elevation to the top of the tower are x and y respectively, where x>y.
Draw a vertical line representing the tower, label the top of the tower as point C and the bottom as point D. Mark points A and B on the horizontal line. The angle of elevation from point A to point C is x and from point B to point C is y.
In triangle ABC (where A is the point on the ground, B is directly below the tower, and C is the top of the tower):
- From point A:
\tan(x) = \frac{h}{d_A} \quad \text{(where d_A isthedistancefrom A to the base of the tower)}
Thus,
dA=htan(x)
- From point B:
\tan(y) = \frac{h}{d_B} \quad \text{(where d_B isthedistancefrom B to the base of the tower)}
Thus,
dB=htan(y)
The distance d between points A and B can be expressed as:
d=dA−dB
Substitute the expressions for dA and dB:
d=htan(x)−htan(y)
To combine the fractions, find a common denominator:
d=h(1tan(x)−1tan(y))=h(tan(y)−tan(x)tan(x)tan(y))
Since x>y, tan(x)>tan(y), thus:
d=h⋅tan(x)−tan(y)tan(x)tan(y)
Therefore, the distance d between the two points is given by:
d=h⋅tan(x)−tan(y)tan(x)tan(y)
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - Self Assessment Sheet - 33
10 Videos
- SIMULTANEOUS LINEAR EQUATIONSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - SIMULTANEOUS LINEAR EQUATIONSEXERCISE - SELF ASSESSMENT SHEET
10 Videos
- SQUARE ROOTS AND CUBE ROOTSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - SQUARE ROOTS AND CUBE ROOTSEXERCISE - SELF ASSESSMENT SHEET-4
10 Videos
Similar Questions
The angle of elevation of the top of a tree of height 18 metres is 30∘ when measured form a point P in the plane of its base. The distance of the base of the tree from P is
View SolutionIf the equations 4x+7y=10 and 10x+ky=25 represent coincident lines then find the value of k?
View SolutionIf √(x−1)(y+2)=7 , x and y being positive whole numbers, then the values of x and y respectively are (a) 8, 5 (b) 15, 12 (c) 22, 19 (d) None of these
View SolutionThe angle of elevation of the top of a tower at a point on the line through the foot of the tower is 45^(@). After walking a distance towards the foot of the tower along the same horizontal line elevation of the top of the tower changes to 60^(@). Find the height of tower.
View SolutionThe angle of elevation of the top of a tower from two points on the ground at distances a metres and b metres from the base of the tower and in the same straight line are complementary.Prove that height of the tower is sqrt(ab).
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
View SolutionHeight of a tower is 100√3 metres. The angle to elevation of the top the tower from a point at a distance of 100 metres of foot of the tower is
View Solutionयदि किसी मीनार के आधार से और एक सरल रेखा में a तथा b दूरी पर स्थित दो बिन्दुओं से मीनार के शीर्ष के उन्नयन कोण पूरक हैं, तो मीनार की ऊँचाई हैं :
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4m and 9m, find the height of the tower from the base of the tower and in the same straight line with it are complementary.
View SolutionThe angle of elevation of the top of a tower of height "h" metres from two points at a distance of "a" and "b" metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is √ab meters.
View SolutionThe angle of elevation of the top of two poles at a point on the line joining the foot of the towers on the ground is 45∘. If the distance between the towers is 1m., the difference between the heights of the tower is
View SolutionThe angles of elevation of the top of a tower from two points at a distances a meter and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is √ab metres.
View SolutionIf the angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary, find the height of the tower.
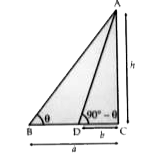
View SolutionA tower is located on a horizontal plane. Two points on a line are a and b at a distance from the base of the tower. The angle between these two points and the lines joining the top of the tower. theta And the elevation angle of the top of the tower from these points alpha And (90^(@) – alpha) If it is the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point A on the ground is 30∘. On moving a distance of 20 metres towards the foot of the tower to a point B, the angle of elevation increases to 60∘. Find the height of the tower and distance of the tower from the point A.
View Solution
