Let 'l' is the length of median from the vertex A to the side BC of a ΔABC. Then Solution in Punjabi
4l2=2b2+2c2−a2
4l2=b2+x2+2bccosA
4l2=a2+4bosA
4l2=(2s−a)2−4bcsin2A2
The correct Answer is:A, B, C, D
Step by step video solution for Let 'l' is the length of median from the vertex A to the side BC of a Delta ABC. Then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:SOLVED EXAMPLES
Explore 1 Video
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise For Sesssion 1
Explore 20 Videos
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 52 Videos
- SEQUENCES AND SERIESBook:ARIHANT MATHSChapter:SEQUENCES AND SERIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 38 Videos
Similar Questions
Match the statements of Column I with values of Column II.

View SolutionIn the given figure,if AB=AC,∠BAD=30∘andAE=AD, then x is equal to
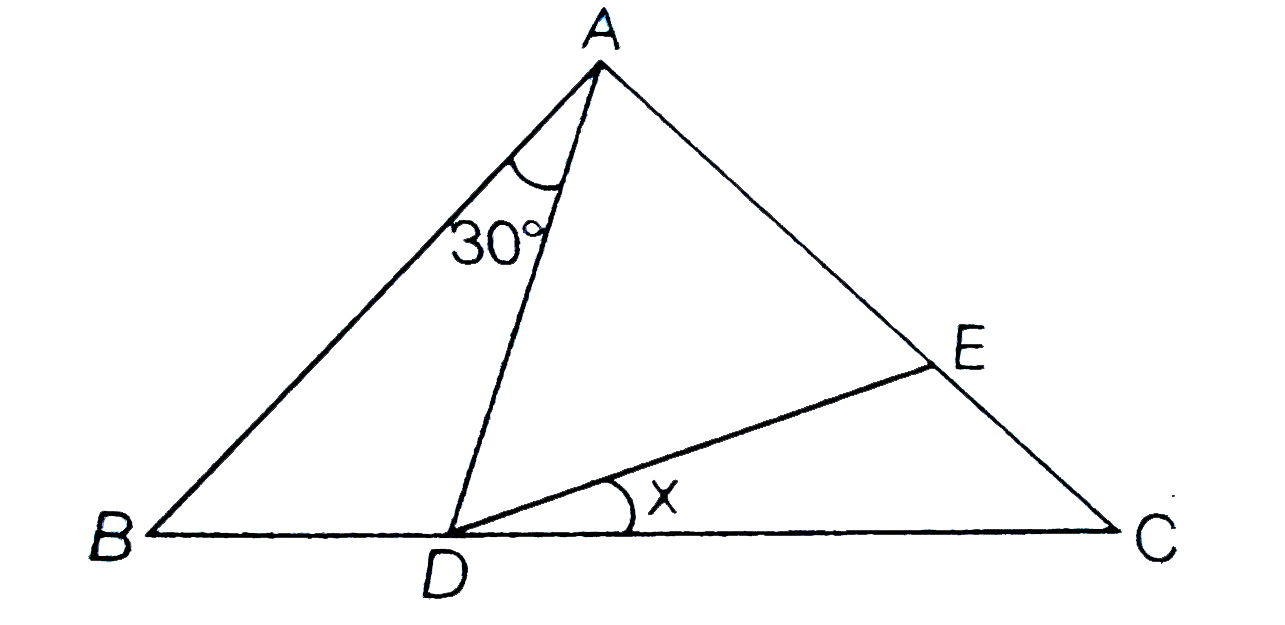
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionIn a Delta ABC, the median to the side BC is of length (1)/(sqrt(11-6sqrt(3))) and it divides the /_A into angles 30^(@) and 45@. Find the length of the side BC.
View SolutionA triangle ABC is such that a circle passing through vertex C, centroid G touches sides AB at B. If AB=6, BC=4 then the length of median through A
View SolutionIf the mid points of the sides BC,CA,AB of a triangle ABC are (-1,3),(-2,4),(2,-5) then the length of the median through vertex A is
View SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If AC = 1, then the length of the median of triangle ABC through the vertex A is equal to
View SolutionLet us consider one vertex and one side through the vertex along x -axis of a triangle . Now the coordinates of the vertices B,C and A of any triangle ABC (0,0) ,(a,0) and (h,k) respectively should be taken .
If in triangle ABC , AC =3 ,BC=4 and median AD is perpendicular with median BE , then the area of ΔABC is -
View SolutionIn a !ABC the length of the median AD to the side BC is 4 units. If ∠A=60∘ and the area of the triangle is 2√3 sq. units. The length of side BC, is
View SolutionIn triangle ABC, AB = AC and the length of median from B to the side AC is l. Find the cosine of angle A for which the area of triangle ABC is maximum.
View SolutionIn ΔABC,AB2+AC2=122andBC=10 Find the length of the median on side BC.
View SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If AC = 1, then the length of the median of triangle ABC through the vertex A is equal to
View SolutionΔABC एक समद्विबाहु त्रिभुज हैं, जिसमें AB=AC=13 सेमी. शीर्ष बिंदु A से भुजा BC पर डाले गए शीर्ष की लम्बाई 5 सेमी. है तो भुजा BC ज्ञात कीजिए।
View SolutionIn △ABC,AB2+AC2=122 and BC=10. Find the length of the median of side BC.
View SolutionIn a triangle ABC, the median to the side BC is of length 1√11−6√3 and it divides A into the angles 30∘ and 45∘ then length of side BC is
View Solution
