Two species of radioactive atoms are mixed in equal number. The disintegration of the first species is λ and of the second is λ/3. After a long time the mixture will behave as a species with mean life of approximately
0.70/λ
2.10/λ
1.00/λ
0.52/λ
The correct Answer is:B
To solve the problem step by step, we need to find the mean life of a mixture of two radioactive species with different disintegration constants.
1. Understanding the Problem:
We have two species of radioactive atoms mixed in equal numbers. The disintegration constant (decay constant) for the first species is denoted as λ, and for the second species, it is λ3.
2. Mean Life Calculation:
The mean life τ of a radioactive species is related to its decay constant λ by the formula:
τ=1λ
Therefore, the mean life for the first species is:
τ1=1λ
And for the second species:
τ2=1λ3=3λ
3. Finding the Average Mean Life:
Since both species are mixed in equal numbers, we can calculate the average mean life τavg of the mixture. The average mean life can be calculated using the formula:
τavg=τ1+τ22
Substituting the values we found:
τavg=1λ+3λ2=4λ2=2λ
4. Final Result:
Therefore, the mean life of the mixture will behave approximately as:
τavg≈2λ
Conclusion:
The mean life of the mixture of the two radioactive species is approximately 2λ.
We have two species of radioactive atoms mixed in equal numbers. The disintegration constant (decay constant) for the first species is denoted as λ, and for the second species, it is λ3.
The mean life τ of a radioactive species is related to its decay constant λ by the formula:
τ=1λ
Therefore, the mean life for the first species is:
τ1=1λ
And for the second species:
τ2=1λ3=3λ
Since both species are mixed in equal numbers, we can calculate the average mean life τavg of the mixture. The average mean life can be calculated using the formula:
τavg=τ1+τ22
Substituting the values we found:
τavg=1λ+3λ2=4λ2=2λ
Therefore, the mean life of the mixture will behave approximately as:
τavg≈2λ
The mean life of the mixture of the two radioactive species is approximately 2λ.
Topper's Solved these Questions
- QUESTION PAPER 2013Book:KVPY PREVIOUS YEARChapter:QUESTION PAPER 2013Exercise:PART-II ( PHYSICS)
Explore 10 Videos
- QUESTION PAPER 2013Book:KVPY PREVIOUS YEARChapter:QUESTION PAPER 2013Exercise:PART-II (PHYSICS)
Explore 5 Videos
- MOCK TEST 9Book:KVPY PREVIOUS YEARChapter:MOCK TEST 9Exercise:EXERCISE
Explore 19 Videos
- QUESTION PAPER 2020Book:KVPY PREVIOUS YEARChapter:QUESTION PAPER 2020Exercise:PART-I : PHYSICS
Explore 50 Videos
Similar Questions
A bullet of mass m is fired horizontally into a large sphere of mass M and radius R resting on a smooth horizontal table.

The bullet hits the sphere at a height h from the table and sticks to its surface. If the sphere starts rolling without slippng immediately on impact, then
View SolutionTwo identical uniform rectangular blocks (with longest side L) and a solid sphere of radius R are to be balanced at the edge of a heavy table such that the centre of the sphere remains at the maximum possible horizontal distance from the vertical edge of the table without toppling as indicated in the figure.
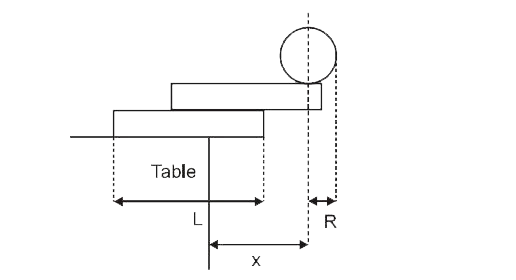
If the mass of each block is M and of the sphere is M/2, then the maximum distance x that can be achieved is
View SolutionA slab of glass, of thickness 6 cm and refractive index μ=1.5 is placed in front of a concave mirror as shown in the figure. If the radius of curvature of the mirror is 40 cm and the reflected image coincides with the object, then the distance of the object from the mirror is

View SolutionA mouse jumps off from the 15th floor of a high-rise building and lands 12 m from the building. Assume that each floor is of 3m height. The horizontal speed with which the mouse jumps is closest to :
View SolutionIf mg of a radioactive species (molar mass M) has decay constant λ The specis activity of sample at t= is given by:
View SolutionThe rate of decay of a radioactive species is given by R_(1) at time t_(1) and R_(2) at later time t_(2) . The mean life of this radioactive species is:
View SolutionIf the rate constant for the disintegration of a radioactive nucleus is lambda . Therefore the probability, P of survival of a radioactive nucleus for one mean life is
View SolutionDisintegration constant of a radioactive material is λ:
View SolutionGiven that radioactive species decays according to the exponential law N=N_(0) e^(-lambda t) . The half life of the species is
View Solutionनिम्न जोड़े में पहली स्पीशीज की आयनन-ऊर्जा, दूसरी स्पीशीज से कम है :
View SolutionIn a radioactive disintegration, the ratio of initial number of atoms to the number of atoms present at an instant of time equal to its mean life is
View SolutionIn a radioactive disintegration, the ratio of initial number oif atoms to the number of atoms present at an instant of tme equal to its mean life is
View SolutionA radioactive sample consists of two distinct species having equal number of atoms initially. The mean life time of one species is τ and that of the other is 5τ. The decay products in both cases are stable. A plot is made of the total number of radioactive nuclei as a function of time. Which of the following figures best represents the form of this plot.
View Solutionनिम्न में से किस युग्म में द्वितीय स्पीशीज की त्रिज्या प्रथम स्पीशीज से कम है :-
View SolutionFind the probability that a certain radioactive atom would get disintegrated in a time equal to the mean life of the radioactive sample.
View SolutionDisintegration constant of a radioactive material is lambda :
View Solution
