ABC is a triangle in which ∠ABC=90∘,BD is perpendicular to AC. Which of the following is TRUE?
I. Triangle BAD is similar to triangle CBD.
II. Triangle BAD is similar to triangle CAB.
III. Triangle BAD is similar to triangle CAB.
Only I
Only II and III
Only I and III
All I, II and III
To solve the problem, we need to analyze the triangles formed in triangle ABC, where angle ABC = 90 degrees and BD is perpendicular to AC. We will check the similarity of the triangles BAD, CBD, and CAB.
1. Identify the Angles in Triangle ABC:
- Given that angle ABC = 90°, we denote angle A as α and angle C as θ.
- Therefore, the angles in triangle ABC are:
- Angle A = α
- Angle B = 90°
- Angle C = θ
- Since the sum of angles in a triangle is 180°, we have:
α+90°+θ=180°
This implies:
α+θ=90°
2. Identify the Angles in Triangle ABD:
- Triangle ABD has:
- Angle A = α (common)
- Angle B = 90° (given)
- Angle D = θ (since angle D is the remaining angle in triangle ABD)
- Thus, the angles in triangle ABD are:
- Angle A = α
- Angle B = 90°
- Angle D = θ
3. Identify the Angles in Triangle CBD:
- Triangle CBD has:
- Angle C = θ (common)
- Angle B = 90° (given)
- Angle D = α (since angle D is the remaining angle in triangle CBD)
- Thus, the angles in triangle CBD are:
- Angle C = θ
- Angle B = 90°
- Angle D = α
4. Check Similarity of Triangles:
- Triangle BAD and Triangle CBD:
- Angle B (BAD) = Angle C (CBD) = 90°
- Angle A (BAD) = Angle D (CBD) = α
- Angle D (BAD) = Angle B (CBD) = θ
- Since two angles of triangle BAD are equal to two angles of triangle CBD, by AA (Angle-Angle) similarity criterion, triangle BAD is similar to triangle CBD.
- Triangle BAD and Triangle CAB:
- Angle B (BAD) = Angle C (CAB) = 90°
- Angle A (BAD) = Angle A (CAB) = α
- Angle D (BAD) = Angle B (CAB) = θ
- Again, by AA similarity criterion, triangle BAD is similar to triangle CAB.
- Triangle BAD and Triangle CAB (Repeated):
- This is the same comparison as above, confirming that triangle BAD is similar to triangle CAB.
5. Conclusion:
- All three statements are true:
- I. Triangle BAD is similar to triangle CBD.
- II. Triangle BAD is similar to triangle CAB.
- III. Triangle BAD is similar to triangle CAB (repeated).
- Therefore, the correct answer is that all statements are true.
Final Answer:
All statements I, II, and III are true.
---
- Given that angle ABC = 90°, we denote angle A as α and angle C as θ.
- Therefore, the angles in triangle ABC are:
- Angle A = α
- Angle B = 90°
- Angle C = θ
- Since the sum of angles in a triangle is 180°, we have:
α+90°+θ=180°
This implies:
α+θ=90°
- Triangle ABD has:
- Angle A = α (common)
- Angle B = 90° (given)
- Angle D = θ (since angle D is the remaining angle in triangle ABD)
- Thus, the angles in triangle ABD are:
- Angle A = α
- Angle B = 90°
- Angle D = θ
- Triangle CBD has:
- Angle C = θ (common)
- Angle B = 90° (given)
- Angle D = α (since angle D is the remaining angle in triangle CBD)
- Thus, the angles in triangle CBD are:
- Angle C = θ
- Angle B = 90°
- Angle D = α
- Triangle BAD and Triangle CBD:
- Angle B (BAD) = Angle C (CBD) = 90°
- Angle A (BAD) = Angle D (CBD) = α
- Angle D (BAD) = Angle B (CBD) = θ
- Since two angles of triangle BAD are equal to two angles of triangle CBD, by AA (Angle-Angle) similarity criterion, triangle BAD is similar to triangle CBD.
- Triangle BAD and Triangle CAB:
- Angle B (BAD) = Angle C (CAB) = 90°
- Angle A (BAD) = Angle A (CAB) = α
- Angle D (BAD) = Angle B (CAB) = θ
- Again, by AA similarity criterion, triangle BAD is similar to triangle CAB.
- This is the same comparison as above, confirming that triangle BAD is similar to triangle CAB.
- All three statements are true:
- I. Triangle BAD is similar to triangle CBD.
- II. Triangle BAD is similar to triangle CAB.
- III. Triangle BAD is similar to triangle CAB (repeated).
- Therefore, the correct answer is that all statements are true.
All statements I, II, and III are true.
Topper's Solved these Questions
Similar Questions
The table shows the production of different types of cars (in thousands).
यह तालिका अलग-अलग प्रकार के कारों का उत्पादन ( हज़ार में) दर्शाती है |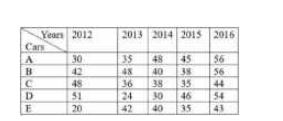 If the data related to the production of cars of type E is represented by a pie chart, then the central angle of the sector
representing the data of production of cars in 2013 will be:
If the data related to the production of cars of type E is represented by a pie chart, then the central angle of the sector
representing the data of production of cars in 2013 will be:
यदि E प्रकार की कारों के उत्पादन से संबंधित आंकड़ों को एक पाई-चार्ट के द्वारा प्रदर्शित किया जाए, तो 2013 में कारों के उत्पादन के आंकड़ों को दर्शाने वाले खंड का केंद्रीय कोण होगा :
View SolutionThe LCM of two No. is 120. Which of the following cannot be HCF of these numbers.
View SolutionABCD is a trapezium in which AB∣∣CD and AD=BC. Show that
(i)∠A=∠B
(ii) ∠C=∠D
(iii) △ABC≅=△BAD
(iv) diagonal AC=diagonal BD

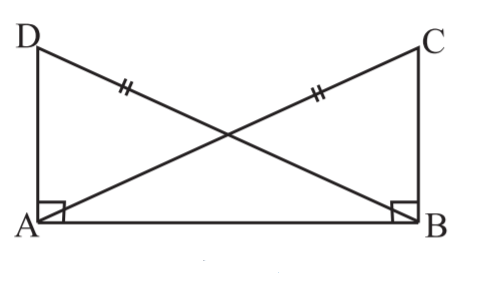
View SolutionIn Fig 7.31, DA⊥AB,CB⊥ABandAC=BD. State the three pairs of equal parts in ΔABCandΔDAB. Which of the following statements is meaningful?
(i) ΔABC≅ΔBAD
(ii) ΔABC≅ABD
View SolutionIf ΔABC~ΔEDFandΔABC is not similar to ΔDEF then which of the following is not ture ?
View Solutionनिम्न प्रश्न में ΔABC,ΔDEF के समरूप है
यदि AC =19 सेमि, तथा DF =8 सेमि, हो तो ΔABC और ΔDEF के क्षेत्रफलों का अनुपात ज्ञात कीजिए|
View SolutionThe ratio of the angles in ΔABC is 2 : 3 : 4. Which of the following triangles is similar to ΔABC ?
View SolutionIn Fig 7.31, DA⊥AB,CB⊥ABandAC=BD. State the three pairs of equal parts in ΔABCandΔDAB. Which of the following statements is meaningful? (i) ΔABC[_≅?]ΔBAD (ii) ΔABC[_≅?]ABD
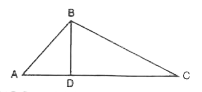
View SolutionΔABC में, ∠B समकोण हैं। भुजा AC पर BD लम्ब हैं, तो सिद्ध कीजिए कि ΔABC के समरूप ΔBDC है।
View Solutionआकृति 7.16 में, AC=BD और AD=BC है! निमिनलखित कथनो में कौन-सा कथन सत्य है?
(i) ΔABC≈ΔABD (ii) ΔABC≈ΔBAD

View Solutionदी गई आकृति में, AC = BD तथा DA⊥AB है। साथ ही CB⊥AB है। बतायें, निम्नलिखित में से कौन-से कथन सत्य है ?
ΔABC=ΔBAD
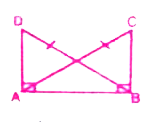
View SolutionΔABC तथा ΔABD में AC = BD और DA⊥AB,CB⊥AB निम्नलिखित में से कौन कथन सत्य है ?
ΔABC≅ΔABC≅ΔBAD
View SolutionWhich of the following is true, in the given figure, where AD is the altitude to the hypotenuse of a right angled △ABC?
△CAD and △ABD are similar
△CDA and △ADB are congruent
△ADB and △CAB are similar
Select the correct answer using the codes given below :
View SolutionIn this ΔABC,BD=8cm,BC=20cm,CD=16cmand∠CBD=∠CAB. Find the perimeter of ΔBDA.
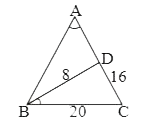
View SolutionABC is a Δ BD = 8 BC = 20 CD = 16 ∠CBD=∠CAB find perimeter of ABC
View Solutionआकृति 7.16 में, AC=BD और AD=BC है। निम्नलिखित कथन सत्य है?
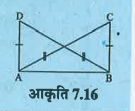 ΔABC≅ΔBAD
ΔABC≅ΔBAD
View Solution