In ΔABC,∠Band∠C are acute angles. BE and CF are perpendicular from vertices B and C on sides AC and AB respectively. Then BC2 is equal to-
AB×BF+AC×CE
AB×BF+AB×CE
AC×BF+AB×BF
BF×CE+AB×AC
To solve the problem, we need to find the expression for BC2 in triangle ABC where BE and CF are the perpendiculars from vertices B and C onto sides AC and AB respectively.
1. Identify the triangles: We have triangle ABC with acute angles B and C. The points E and F are the feet of the perpendiculars from B to AC and from C to AB respectively.
2. Apply the Pythagorean theorem in triangle ABE:
AB2=AE2+BE2
Here, AE=AC−CE, so we can express AE as:
AE=AC−CE
Therefore, substituting AE:
AB2=(AC−CE)2+BE2
3. Expand the equation:
AB2=(AC2−2AC⋅CE+CE2)+BE2
This simplifies to:
AB2=AC2+CE2+BE2−2AC⋅CE
4. Apply the Pythagorean theorem in triangle ACF:
AC2=AF2+CF2
Here, AF=AB−BF, so:
AC2=(AB−BF)2+CF2
5. Expand this equation:
AC2=(AB2−2AB⋅BF+BF2)+CF2
This simplifies to:
AC2=AB2+BF2+CF2−2AB⋅BF
6. Apply the Pythagorean theorem in triangle BCF:
BC2=BF2+CF2
7. Combine the equations: We now have expressions for AB2 and AC2 that include BF2 and CF2. We can add these equations together:
AB2+AC2=(AC2+CE2+BE2−2AC⋅CE)+(AB2+BF2+CF2−2AB⋅BF)
8. Rearranging the terms: After adding, we can isolate BC2:
2BC2=AB2+AC2−2AB⋅BF−2AC⋅CE
Dividing by 2 gives:
BC2=12(AB⋅BF+AC⋅CE)
Final Result:
Thus, we conclude that:
BC2=AB⋅BF+AC⋅CE
AB2=AE2+BE2
Here, AE=AC−CE, so we can express AE as:
AE=AC−CE
Therefore, substituting AE:
AB2=(AC−CE)2+BE2
AB2=(AC2−2AC⋅CE+CE2)+BE2
This simplifies to:
AB2=AC2+CE2+BE2−2AC⋅CE
AC2=AF2+CF2
Here, AF=AB−BF, so:
AC2=(AB−BF)2+CF2
AC2=(AB2−2AB⋅BF+BF2)+CF2
This simplifies to:
AC2=AB2+BF2+CF2−2AB⋅BF
BC2=BF2+CF2
AB2+AC2=(AC2+CE2+BE2−2AC⋅CE)+(AB2+BF2+CF2−2AB⋅BF)
2BC2=AB2+AC2−2AB⋅BF−2AC⋅CE
Dividing by 2 gives:
BC2=12(AB⋅BF+AC⋅CE)
Thus, we conclude that:
BC2=AB⋅BF+AC⋅CE
Topper's Solved these Questions
Similar Questions
The table shows the production of different types of cars (in thousands).
यह तालिका अलग-अलग प्रकार के कारों का उत्पादन ( हज़ार में) दर्शाती है |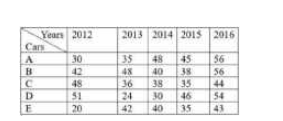 If the data related to the production of cars of type E is represented by a pie chart, then the central angle of the sector
representing the data of production of cars in 2013 will be:
If the data related to the production of cars of type E is represented by a pie chart, then the central angle of the sector
representing the data of production of cars in 2013 will be:
यदि E प्रकार की कारों के उत्पादन से संबंधित आंकड़ों को एक पाई-चार्ट के द्वारा प्रदर्शित किया जाए, तो 2013 में कारों के उत्पादन के आंकड़ों को दर्शाने वाले खंड का केंद्रीय कोण होगा :
View SolutionThe LCM of two No. is 120. Which of the following cannot be HCF of these numbers.
View SolutionIn ΔABC,∠B=∠C. Prove the perpendiculars from the mid-point of BC and AC are equal.
View SolutionIn a △ABC the angles at B and C are acute. If BE and CF be drawn perpendiculars on AC and AB respectivel, prove that
BC2=Ab×BF+AC×EC
View Solutionआकृति में, ΔABC का ∠B न्यूनकोण है और AD⊥BC| सिद्ध कीजिए कि
AC2=AB2+BC2−2BC.BD.
View Solutionयदि AB=AC है तथा BE और CF क्रमशः ∠Bऔर ∠Cके समद्विभाजक हैं, तो सिध्द करो कि ΔEBC≅ΔFCB.
View SolutionΔABC में, ∠B=∠C है। सिद्ध कीजिए कि BC के माध्य-बिन्दु से AB और AC पर डाले गये लम्ब बराबर है।
View SolutionΔABC में ∠A=120∘ एवं AB=AC तो ∠B और ∠C में से प्रत्येक बराबर है
View SolutionIn ΔABC, AB=BC=AC then ∠A=∠B=∠C=…….
View SolutionΔABC में AB = AC और ∠B=50∘ है तब ∠C बराबर है :
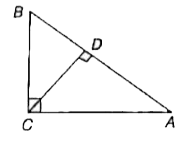
View SolutionIn a right angled ΔABC,∠C=90∘andCD is the perpendicular on the hypotenuse AB,AB=c,BC=a,AC=bandCD=p, then :
View SolutionΔABCमेंAB=ACऔर∠B=45∘तो∠C बराबर है-
View SolutionΔABCमेंAB=ACऔर∠B=45∘तो∠A बराबर है-
View SolutionΔABC में, यदि BC = AB और ∠C=80∘ तब ∠A=...
View SolutionIn ΔABC,∠B=∠C. Prove the perpendiculars from the mid-point of BC to AB and AC are equal.
View Solution
