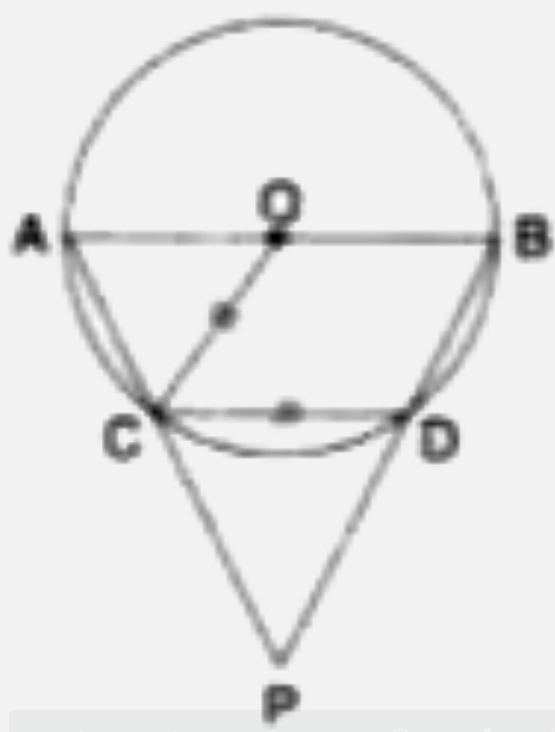
In a circle with centre O, AB is a diameter and CD is a chord which is equal to the radius OC. AC and BD are extended in such a way that they intersect each other at a point P, exterior to the circle. The measure of ∠APB is
30∘
45∘
60∘
90∘
To solve the problem, we need to find the measure of angle ∠APB given that AB is a diameter of the circle, CD is a chord equal to the radius OC, and AC and BD are extended to intersect at point P outside the circle.
1. Identify the Elements:
- Let the center of the circle be O.
- AB is the diameter of the circle.
- C and D are points on the circle such that CD=OC (the radius).
2. Understand the Geometry:
- Since AB is a diameter, by the Inscribed Angle Theorem, any angle inscribed in a semicircle is a right angle. Therefore, ∠ACB=90∘.
3. Analyze Triangle OCD:
- Since OC and OD are both radii of the circle, we have OC=OD.
- Given CD=OC, triangle OCD is an equilateral triangle (since all sides are equal).
- Therefore, each angle in triangle OCD is 60∘.
4. Determine Angles at Point P:
- Extend lines AC and BD to meet at point P.
- We know that ∠ACB=90∘ and ∠OCD=60∘.
- The angles ∠ACP and ∠BDP can be expressed in terms of ∠APB.
5. Use the Exterior Angle Theorem:
- The exterior angle ∠APB is equal to the sum of the opposite interior angles ∠ACP and ∠BDP.
- Since ∠ACB=90∘ and ∠OCD=60∘, we can express ∠APB as:
∠APB=∠ACB+∠OCD=90∘+60∘=150∘
6. Conclusion:
- Therefore, the measure of ∠APB is 150∘.
- Let the center of the circle be O.
- AB is the diameter of the circle.
- C and D are points on the circle such that CD=OC (the radius).
- Since AB is a diameter, by the Inscribed Angle Theorem, any angle inscribed in a semicircle is a right angle. Therefore, ∠ACB=90∘.
- Since OC and OD are both radii of the circle, we have OC=OD.
- Given CD=OC, triangle OCD is an equilateral triangle (since all sides are equal).
- Therefore, each angle in triangle OCD is 60∘.
- Extend lines AC and BD to meet at point P.
- We know that ∠ACB=90∘ and ∠OCD=60∘.
- The angles ∠ACP and ∠BDP can be expressed in terms of ∠APB.
- The exterior angle ∠APB is equal to the sum of the opposite interior angles ∠ACP and ∠BDP.
- Since ∠ACB=90∘ and ∠OCD=60∘, we can express ∠APB as:
∠APB=∠ACB+∠OCD=90∘+60∘=150∘
- Therefore, the measure of ∠APB is 150∘.
Topper's Solved these Questions
Similar Questions
The table shows the production of different types of cars (in thousands).
यह तालिका अलग-अलग प्रकार के कारों का उत्पादन ( हज़ार में) दर्शाती है |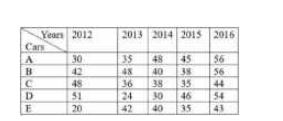 If the data related to the production of cars of type E is represented by a pie chart, then the central angle of the sector
representing the data of production of cars in 2013 will be:
If the data related to the production of cars of type E is represented by a pie chart, then the central angle of the sector
representing the data of production of cars in 2013 will be:
यदि E प्रकार की कारों के उत्पादन से संबंधित आंकड़ों को एक पाई-चार्ट के द्वारा प्रदर्शित किया जाए, तो 2013 में कारों के उत्पादन के आंकड़ों को दर्शाने वाले खंड का केंद्रीय कोण होगा :
View SolutionThe LCM of two No. is 120. Which of the following cannot be HCF of these numbers.
View SolutionIn Fig. 10.32, AB is a diameter of the circle, CD is a chord equal to theradius of the circle. AC and BD when extended intersect at a point E. Prove that∠AEB = 60∘
View SolutionIn Figure, AB is a diameter of a circle C(O, r). Chord CD is equal to radius OC. If AC and BD when produced intersect at P, prove that ∠APB is constant.
View Solutionकिसी वृत्त का केंद्र O है, AB व्यास है और CD चापकर्ण है जोकि OC त्रिज्या के बराबर है। AC और BD को इस प्रकार बढ़ाया जाता है कि वे एक-दूसरे को बिंदु P पर काटते है जोकि वृत्त के बाहर है। ∠APB का माप क्या होगा?
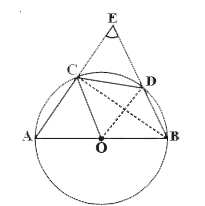
View SolutionAB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
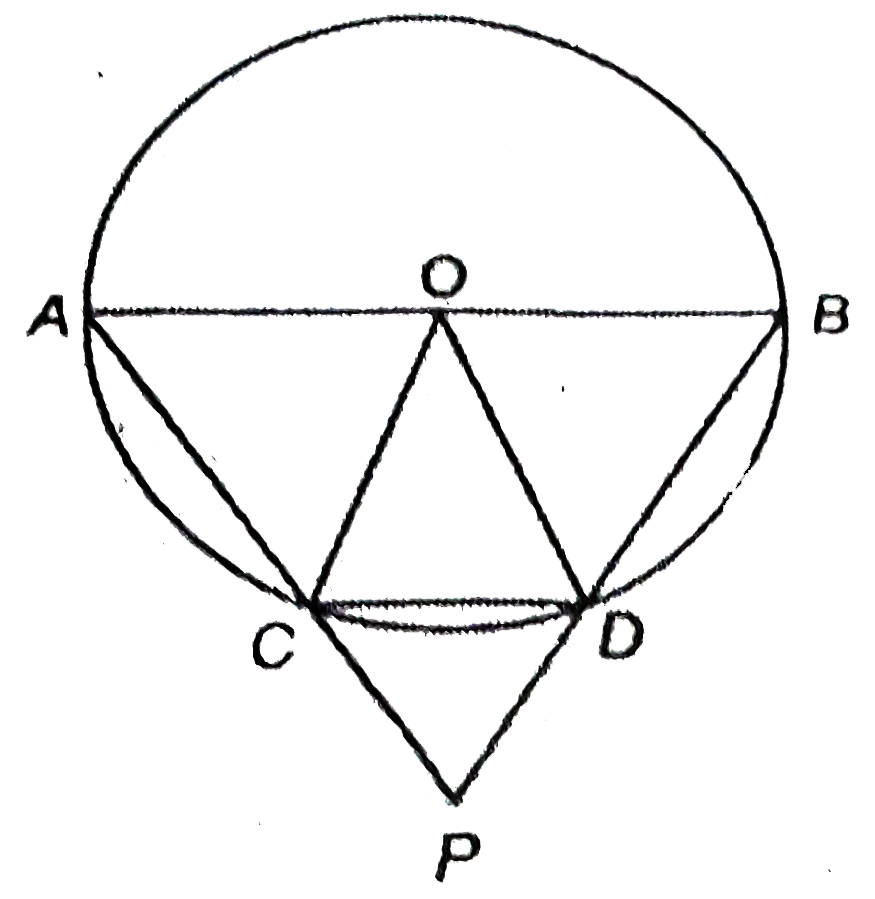
View SolutionIn the adjoining figure,AB is the diameter of the circle of centre O & the chord CD is equal to radius. If P is an external point, then find the value of ∠APB.
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View Solutionसंलग्न चित्र में, AB वृत्त का व्यास है | जीवा CD वृत्त की त्रिज्या के बराबर है | AC और BD बढ़ाने पर बिन्दु E पर प्रतिच्छेद करते हैं | सिद्ध कीजिए कि ∠AEB=60∘ है |
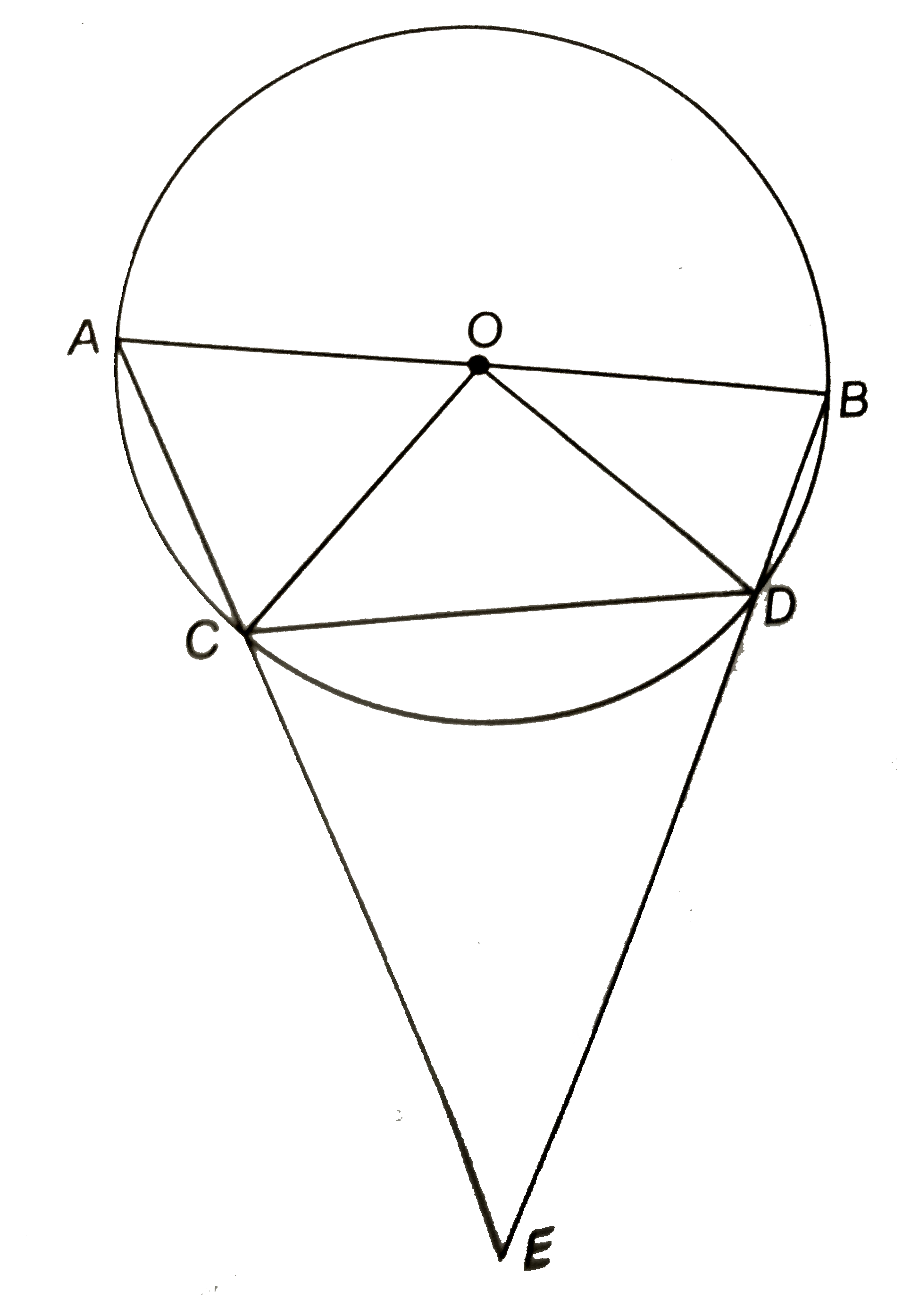
View SolutionIn the adjoining figure, O is the centre of a circle and AB is one of its diameters. The legth of the chrod CD is equal to the radius of the circle. When AC and BD are extended, they intersect each other at a point P. find the value of ∠APB
View SolutionIn figure, ¯¯¯¯¯¯AB is a diameter of the circle, ¯¯¯¯¯¯CD is a chord equal to the radius of the circle. ¯¯¯¯¯¯AC and ¯¯¯¯¯¯BD when extended intersect at a point E. Prove that ∠AEB=6∘.
View SolutionThe center of the circle O and the diameter AB in the side figure. The length of the chord CD is equal to the length of the radius of the circle. As AC and BD increase, it intersects at point P. angleAPB Let's determine the value of.
View SolutionAB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Find the ∠AEB.
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DP
View SolutionAB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : ∠APB=60∘
View SolutionAB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.

View Solution
